在非等边三角形 $ABC$ 中,$CA=CB$,若 $O,P $ 分别为 $ \triangle ABC $ 的外心和内心,点 $ D $ 在线段 $ BC $ 上,且满足 $ OD\perp BP$,则下列的说法正确的是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
AD
【解析】
由 $\angle HOP=\angle ABP=\angle PBD$ 得 $BDOP$ 四点共圆,故 $A$ 正确;
由于三角形不等边,故 $AC$ 与 $BP$ 不垂直,而 $OD\perp BP$,所以 $OD$ 与 $AC$ 不平行,因此 $B$ 错误;
$C$ 显然不对 $\ldots \ldots $
由 $A$ 中四点共圆知:$$\angle BDP=\angle BOP=\angle BCO+\angle OBC=2\angle BCO=\angle BCA$$故 $PD\parallel AC$,即 $D$ 正确.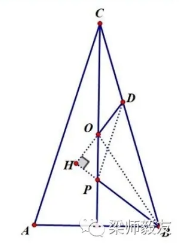
由于三角形不等边,故 $AC$ 与 $BP$ 不垂直,而 $OD\perp BP$,所以 $OD$ 与 $AC$ 不平行,因此 $B$ 错误;
$C$ 显然不对 $\ldots \ldots $
由 $A$ 中四点共圆知:$$\angle BDP=\angle BOP=\angle BCO+\angle OBC=2\angle BCO=\angle BCA$$故 $PD\parallel AC$,即 $D$ 正确.

题目
答案
解析
备注