在直角 $\triangle ABC$ 中,$\angle ABC=90^{\circ}, AB=\sqrt{3}, BC=1$,且 $\frac{\overrightarrow{PA}}{|\overrightarrow{PA}|}+\frac{\overrightarrow{PB}}{|\overrightarrow{PB}|}+\frac{\overrightarrow{PC}}{|\overrightarrow{PC}|}=\overrightarrow{0}$,则下列说法正确的是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
ABCD
【解析】
由题意,$\overrightarrow{PA}, \overrightarrow{PB}, \overrightarrow{PC}$ 两两夹角 $120^{\circ}$,故 $A, B$ 均正确;
如图,$P$ 为费马点,由 $\triangle BPC~ \triangle BCA'$ 得 $\frac{PC}{PB}=\frac{A'C}{BC}=\frac{AC}{BC}=2$,$C$ 正确;
由 $\triangle APC~\triangle ACB'$ 得 $\frac{PA}{PC}=\frac{AC}{B'C}=\frac{AC}{BC}$,$D$ 正确.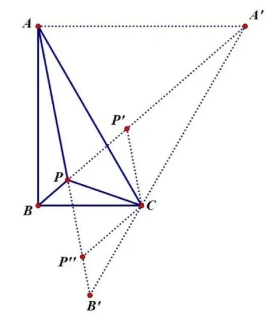
如图,$P$ 为费马点,由 $\triangle BPC~ \triangle BCA'$ 得 $\frac{PC}{PB}=\frac{A'C}{BC}=\frac{AC}{BC}=2$,$C$ 正确;
由 $\triangle APC~\triangle ACB'$ 得 $\frac{PA}{PC}=\frac{AC}{B'C}=\frac{AC}{BC}$,$D$ 正确.

题目
答案
解析
备注