已知正三棱锥侧面与底面所成二面角的余弦值为 $\frac{1}{6}$，则此三棱锥的高 $h$ 与其内切求半径 $r$ 之比是 \((\qquad)\) ．
【难度】
【出处】
无
【标注】
【答案】
【解析】
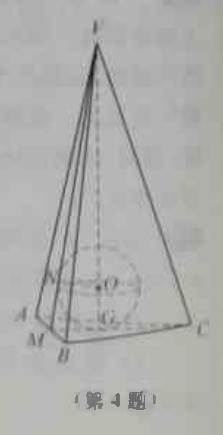如图，过正三棱锥 $V-ABC$ 的侧棱 $VC$ 及高 $VG$ 作截面交 $AB$ 于点 $M$，则内切球 $O$ 与侧面相切的切点 $N$ 在 $VM$ 上．在 $\triangle VGM$ 中，$$\frac{ON}{VO}=\frac{GM}{VM}=\frac{1}{6}.$$故 $\frac{r}{h-r}=\frac{1}{6}$，得到 $\frac{h}{r}=7$．
题目
答案
解析
备注
