在三棱锥 $P-ABC$ 中，$PA\perp ABC$，$AC\perp BC$，$AC=2$，二面角 $P-BC-A$ 的大小为 $60^\circ$，三棱锥 $P-ABC$ 的体积为 $\dfrac{4\sqrt 6}3$，则直线 $PB$ 与平面 $PAC$ 所成的角的正弦值为 \((\qquad)\)
【难度】
【出处】
2014年卓越联盟自主招生试题
【标注】
【答案】
C
【解析】
因为二面角 $P-BC-A$ 的平面角为 $\angle PCA$，所以在直角 $\triangle PAC$ 中，有 $PA=2\sqrt 3$．
又因为 $V_{P-ABC}=\dfrac 13\cdot\dfrac 12\cdot AC\cdot BC\cdot PA$，解得 $BC=2\sqrt 2$，从而有 $PB=2\sqrt 6$，如图：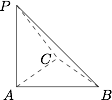
直线 $PB$ 与平面 $PAC$ 所成的角为 $\angle BPC$，所以$$\sin\angle BPC=\dfrac {BC}{PB}=\dfrac {\sqrt 3}3.$$
又因为 $V_{P-ABC}=\dfrac 13\cdot\dfrac 12\cdot AC\cdot BC\cdot PA$，解得 $BC=2\sqrt 2$，从而有 $PB=2\sqrt 6$，如图：
直线 $PB$ 与平面 $PAC$ 所成的角为 $\angle BPC$，所以$$\sin\angle BPC=\dfrac {BC}{PB}=\dfrac {\sqrt 3}3.$$
题目
答案
解析
备注
