已知函数 $f(x)=|\ln x|$，$g(x)=\begin{cases} 0, 0<x\leqslant 1,\\\big|x^2-4\big|-2,x>1,\end{cases}$ 则方程 $\big|f(x)+g(x)\big|=1$ 实根的个数为 ．
【难度】
【出处】
2015年高考江苏卷
【标注】
【答案】
$4$
【解析】
根据题意，有$$f(x)+g(x)=\begin{cases} -\ln x,0<x\leqslant 1,\\\ln x+|x^2-4|-2,x>1,\end{cases}$$也即$$f(x)+g(x)=\begin{cases}-\ln x,0<x\leqslant 1,\\\ln x+2-x^2,1<x\leqslant 2,\\\ln x+x^2-6,x>2.\end{cases}$$显然，该函数在 $(0,1]$ 上单调递减，在 $(2,+\infty )$ 上单调递增．而在 $(1,2]$ 上，导函数为$$\left(f(x)+g(x)\right)'=\dfrac 1x-2x=\dfrac 1x(1-2x^2)<0,$$因此该函数在 $(1,2]$ 上单调递减，函数图象如图．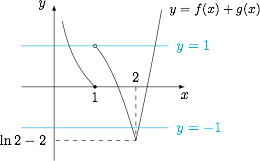
因此题中方程的实根个数为 $4$．
因此题中方程的实根个数为 $4$．
题目
答案
解析
备注
