如图，平面直角坐标系中，将含 $30^\circ $ 的三角尺的直角顶点 $C$ 落在第二象限．其斜边两端点 $A,B$ 分别落在 $x,y$ 轴上，且 $AB=12 {\mathrm {cm}}$．则点 $C$ 与点 $O$ 的距离的最大值为 $\rm{cm}$．
【难度】
【出处】
无
【标注】
【答案】
$12$
【解析】
如图，取 $BC$ 的中点 $D$，连接 $CD,OD,CO$．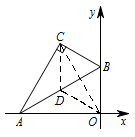
则 $CD=OD=\dfrac 12AB=6 \rm{cm}$．
而 $CO\leqslant CD+OD=12 \rm{cm}$，
所以 $CO$ 的最大值为 $12 rm{cm}$，此时点 $D$ 在 $CO$ 上．
则 $CD=OD=\dfrac 12AB=6 \rm{cm}$．而 $CO\leqslant CD+OD=12 \rm{cm}$，
所以 $CO$ 的最大值为 $12 rm{cm}$，此时点 $D$ 在 $CO$ 上．
题目
答案
解析
备注
