正三棱锥 $P-ABC$ 中，$AB=1,AP=2$，过 $AB$ 的平面 $\alpha$ 将其体积平分，则棱 $PC$ 与平面 $\alpha$ 所成角的余弦值为 ．
【难度】
【出处】
2017年全国高中数学联赛A卷（一试）
【标注】
【答案】
$\dfrac{3\sqrt 5}{10}$
【解析】
根据题意，平面 $\alpha$ 与棱 $PC$ 交于 $PC$ 的中点 $M$，设 $N$ 为 $AB$ 的中点，如图．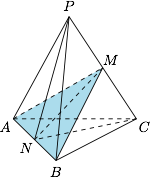
由平行四边形的性质可得\[AM^2=\dfrac 12\left(AP^2+AC^2\right)-\dfrac 14PC^2=\dfrac 32,\]进而\[MN=\sqrt{AM^2-\left(\dfrac 12AB\right)^2}=\dfrac{\sqrt 5}2.\]由于 $CN$ 过底面中心，因此平面 $PNC$ 包含过 $P$ 的底面垂线，因此 $PC$ 在平面 $\alpha$ 内的投影为 $MN$，于是\[\cos\langle PC,MN\rangle =\left|\dfrac{MN^2+MC^2-CN^2}{2\cdot MN\cdot MC}\right|=\dfrac{3\sqrt{5}}{10}.\]
由平行四边形的性质可得\[AM^2=\dfrac 12\left(AP^2+AC^2\right)-\dfrac 14PC^2=\dfrac 32,\]进而\[MN=\sqrt{AM^2-\left(\dfrac 12AB\right)^2}=\dfrac{\sqrt 5}2.\]由于 $CN$ 过底面中心，因此平面 $PNC$ 包含过 $P$ 的底面垂线，因此 $PC$ 在平面 $\alpha$ 内的投影为 $MN$，于是\[\cos\langle PC,MN\rangle =\left|\dfrac{MN^2+MC^2-CN^2}{2\cdot MN\cdot MC}\right|=\dfrac{3\sqrt{5}}{10}.\]
题目
答案
解析
备注
