查看数据源：60bed95a95a31e000a975ed0
在正方体 $ABCD-A_1B_1C_1D_1$ 中，$P$ 为 $B_1D_1$ 的中点，则直线 $PB$ 与 $AD_1$ 所成的角为 \((\qquad)\) ．
A: $\frac{\pi}{2}$
B: $\frac{\pi}{3}$
C: $\frac{\pi}{4}$
D: $\frac{\pi}{6}$
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
如图，$\angle PBC_1$ 为直线 $PB$ 与 $AD_1$ 所成角的平面角．
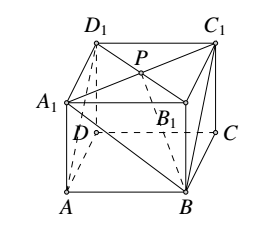
易知 $\triangle A_1BC_1$ 为正三角形，又 $P$ 为 $A_1C_1$ 中点，所以 $\angle PBC_1=\frac{\pi}{6}$．
题目 答案 解析 备注
0.114533s