在平面直角坐标系 $xOy$，点集 $K=\{(x,y)\mid x,y\in -1,0,1\}$．在 $K$ 中随机取出三个点，则这三个点两两之间的距离均不超过 $2$ 的概率是 ．
【难度】
【出处】
2017年全国高中数学联赛B卷（一试）
【标注】
【答案】
$\dfrac 5{14}$
【解析】
如图，点集 $K=\{O,P_1,P_2,P_3,P_4,P_5,P_6,P_7,P_8\}$．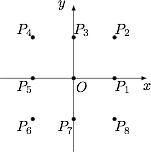
三个点两两之间的距离可能为 $1,\sqrt 2,2,\sqrt5,2\sqrt 2$．因此有如下情形．
情形一 两两之间的距离为 $1,1,\sqrt 2$，共有 $16$ 个．
情形二 两两之间的距离为 $1,1,2$，共有 $6$ 个．
情形三 两两之间的距离为 $\sqrt 2,\sqrt 2,2$，共有 $8$ 个．
综上所述．所求的概率为\[\dfrac{16+6+8}{{\rm C}_9^3}=\dfrac{30}{84}=\dfrac{5}{14}.\]
三个点两两之间的距离可能为 $1,\sqrt 2,2,\sqrt5,2\sqrt 2$．因此有如下情形．综上所述．所求的概率为\[\dfrac{16+6+8}{{\rm C}_9^3}=\dfrac{30}{84}=\dfrac{5}{14}.\]
题目
答案
解析
备注
