在区间 $(0,1)$ 与 $(1,2)$ 中各随机取 $1$ 个数,则两数之和大于 $\frac{7}{4}$ 的概率为 \((\qquad)\) .
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
由题记 $x\in(0,1), y\in (1,2)$,题目即求 $x+y>\frac{7}{4}$ 的概率.绘图如下所示.
故 $P=\frac{S_{\text{阴}}}{S_{\text{正}ABCD}}=\frac{1\times 1-\frac{1}{2}AM\cdot AN}{1\times 1}=\frac{1-\frac{1}{2}\times \frac{3}{4}\times \frac{3}{4}}{1}=\frac{23}{32}$.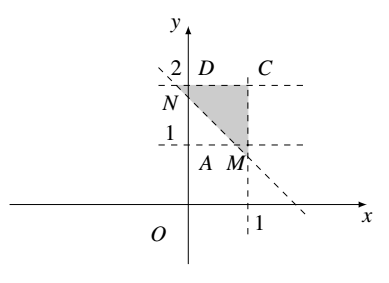
故 $P=\frac{S_{\text{阴}}}{S_{\text{正}ABCD}}=\frac{1\times 1-\frac{1}{2}AM\cdot AN}{1\times 1}=\frac{1-\frac{1}{2}\times \frac{3}{4}\times \frac{3}{4}}{1}=\frac{23}{32}$.

题目
答案
解析
备注