已知 $f(x)$ 是定义在 $\mathbb R$ 上的周期为 $2$ 的偶函数，且当 $x\in [0,1]$ 时，$f(x)=x+1$，则方程 $f^2(x)+f(x)=x$ 的根的个数为 ．
【难度】
【出处】
无
【标注】
【答案】
$4$
【解析】
可以将方程 $f^2(x)+f(x)=x$ 的根的个数即函数 $y=f(x)$ 的图象与方程 $y^2+y=x$ 的曲线的交点的横坐标的不同取值个数，也即交点个数．
根据函数 $f(x)$ 的奇偶性与周期性，作图如下．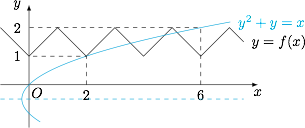
注意到抛物线 $y^2+y=x$ 以 $\left(-\dfrac 14,-\dfrac 12\right)$ 为顶点，以 $y=-\dfrac 12$ 为对称轴，且经过点 $(0,0)$，$(2,1)$，$(6,2)$，因此抛物线 $y^2+y=x$ 与函数 $y=f(x)$ 的图象共有 $4$ 个交点，所求的根的个数为 $4$．
根据函数 $f(x)$ 的奇偶性与周期性，作图如下．
注意到抛物线 $y^2+y=x$ 以 $\left(-\dfrac 14,-\dfrac 12\right)$ 为顶点，以 $y=-\dfrac 12$ 为对称轴，且经过点 $(0,0)$，$(2,1)$，$(6,2)$，因此抛物线 $y^2+y=x$ 与函数 $y=f(x)$ 的图象共有 $4$ 个交点，所求的根的个数为 $4$．
题目
答案
解析
备注
