利用直线 $y=-\dfrac 13x$ 建立动区间 $[-1,t]$ 和动直线 $y=-\dfrac 13t$ 之间的联系，然后计算临界点，分段讨论．
如图，设直线 $y=-\dfrac 13x$ 与函数 $f(x)=x^3-x$ 的图象交于 $A,O,B$ 三点，与函数 $y=f(x)$ 的水平切线交于 $M,N$ 两点．不难计算得 $A\left(-\dfrac{\sqrt 6}3,\dfrac{\sqrt 6}9\right)$，$B\left(\dfrac{\sqrt 6}3,-\dfrac{\sqrt 6}9\right)$，$M\left(-\dfrac{2\sqrt 3}3,\dfrac{2\sqrt 3}9\right)$，$N\left(\dfrac{2\sqrt 3}3,\dfrac{2\sqrt 3}9\right)$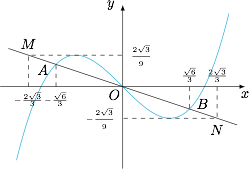．利用图象可知：
情形一当 $-1<t<-\dfrac{\sqrt 6}3$ 时，方程没有实根；
情形二当 $-\dfrac{\sqrt 6}3\leqslant t<0$ 时，方程有 $1$ 个实根；
情形三当 $t=0$ 时，方程有 $2$ 个实根；
情形四当 $0<t<\dfrac{\sqrt 6}3$ 时，方程有 $1$ 个实根；
情形五当 $\dfrac{\sqrt 6}3\leqslant t<\dfrac{2\sqrt 3}3$ 时，方程有 $2$ 个实根；
情形六当 $t=\dfrac{2\sqrt 3}3$ 时，方程有 $1$ 个实根；
情形七当 $t>\dfrac{2\sqrt 3}3$ 时，方程没有实根．
综上所述，$t$ 的取值范围是 $\left[-\dfrac{\sqrt 6}3,0\right)\cup\left(0,\dfrac{\sqrt 6}3\right)\cup\left\{\dfrac{2\sqrt 3}3\right\}$．