集合 $A=\{1,2,\cdots ,n\}$,则定义在 $A$ 上的不减函数 $f:A\to A$(即 $\forall x,y\in A,x\leqslant y,$ 有 $f(x)\leqslant f(y)$)的个数为 .
【难度】
【出处】
无
【标注】
【答案】
${\mathrm C}_{2n-1}^{n}$
【解析】
考虑 $(n+1) \times n$ 的网格,每一个符合题意的不减函数都与其中的路径$$(1,f(1))\to (2,f(2))\to \cdots \to (n,f(n))$$一一对应,将路径补充为$$(1,1)\to (1,f(1))\to (2,f(2))\to \cdots \to (n,f(n)) \to (n+1,n)$$且将该路径看作沿网格中的线段从 $(1,1)$ 运动到 $(n+1,n)$,每次只能往右或者往上运动.因此只需要在总共的 $2n-1$ 次运动中确定向右运动的那 $n$ 次的位置即可,答案为 ${\rm C}_{2n-1}^{n}$.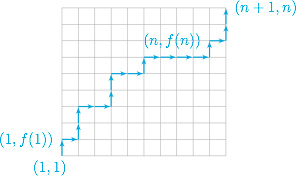

题目
答案
解析
备注