已知函数 $f(x)=\sqrt{10-6\cos x}+\sqrt{\dfrac{17}8-\dfrac{3\sqrt 2}2\sin x}+\sqrt{19-2\sqrt 2\cos x-8\sin x}$，则 $f(x)$ 的最小值为 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{21\sqrt 2}{4}-1$
【解析】
先对 $f(x)$ 的各个根式进行配方，尝试寻找几何意义：$$f(x)=\sqrt{(\cos x-3)^2+\sin^2x}+\sqrt{\cos^2x+\left(\sin x-\dfrac{3\sqrt 2}4\right)^2}+\sqrt{(\cos x-\sqrt 2)^2+(\sin x-4)^2},$$因此 $f(x)$ 表示单位圆上的点 $P(\cos x,\sin x)$ 到点 $A(3,0)$，$B\left(0,\dfrac{3\sqrt 2}4\right)$，$C(\sqrt 2,4)$ 的距离之和．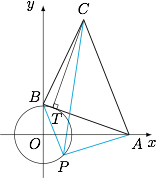
如图，注意到原点 $O$ 到直线 $AB:\dfrac 13x+\dfrac {2\sqrt 2}3y=1$ 的距离为$$\dfrac{1}{\sqrt{\left(\dfrac 13\right)^2+\left(\dfrac{2\sqrt 2}3\right)^2}}=1,$$于是直线 $AB$ 与单位圆相切，设切点为 $T$．又 $OC$ 的斜率为 $2\sqrt 2$，$AB$ 的斜率为 $-\dfrac{\sqrt 2}4$，于是 $OC\perp AB$．又因为 $OT\perp AB$，所以 $O,C,T$ 三点共线，从而有 $PA+PB\geqslant TA+TB$，且 $PC\geqslant TC$，因此所求的最小值为$$\begin{split} TA+TB+TC=&AB+TC\\=&\dfrac{9\sqrt 2}4+\dfrac{\dfrac 13\cdot \sqrt 2+\dfrac{2\sqrt 2}3\cdot 4-1}{\sqrt{\left(\dfrac 13\right)^2+\left(\dfrac{2\sqrt 2}3\right)^2}}\\=&\dfrac{21\sqrt 2}{4}-1.\end{split} $$
如图，注意到原点 $O$ 到直线 $AB:\dfrac 13x+\dfrac {2\sqrt 2}3y=1$ 的距离为$$\dfrac{1}{\sqrt{\left(\dfrac 13\right)^2+\left(\dfrac{2\sqrt 2}3\right)^2}}=1,$$于是直线 $AB$ 与单位圆相切，设切点为 $T$．又 $OC$ 的斜率为 $2\sqrt 2$，$AB$ 的斜率为 $-\dfrac{\sqrt 2}4$，于是 $OC\perp AB$．又因为 $OT\perp AB$，所以 $O,C,T$ 三点共线，从而有 $PA+PB\geqslant TA+TB$，且 $PC\geqslant TC$，因此所求的最小值为$$\begin{split} TA+TB+TC=&AB+TC\\=&\dfrac{9\sqrt 2}4+\dfrac{\dfrac 13\cdot \sqrt 2+\dfrac{2\sqrt 2}3\cdot 4-1}{\sqrt{\left(\dfrac 13\right)^2+\left(\dfrac{2\sqrt 2}3\right)^2}}\\=&\dfrac{21\sqrt 2}{4}-1.\end{split} $$
题目
答案
解析
备注
