注意到$$f\left(-\dfrac 13\right)=\dfrac 19-\dfrac 13(a-3b),$$于是 $a-3b=\dfrac 13-3f\left(-\dfrac 13\right)$，因此只要求出 $f\left(-\dfrac 13\right)$ 的取值范围，就求出了 $a-3b$ 的取值范围．我们猜测 $f\left(-\dfrac 13\right)$ 的最小值和最大值分别如下左图和右图时取得（注意，因为 $x^{2}$ 前面的系数确定，所以抛物线形状固定，只能左右上下平移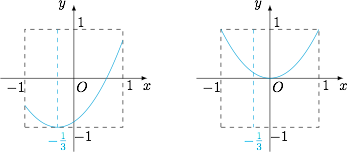）．接下来，我们进行论证．显然有 $f\left(-\dfrac 13\right)\geqslant -1$，且当 $f(x)=\left(x+\dfrac 13\right)^2-1$ 时等号可以取得，这样就得到了 $a-3b\leqslant \dfrac {10}3$．而对于 $a-3b$ 的最小值，注意到此时 $f(1)=f(-1)=1$，因此抓住这点进行论证．事实上，有$$\begin{cases} f(1)=1+a+b,\\ f(-1)=1-a+b,\end{cases}$$因此 $a=\dfrac 12f(1)-\dfrac 12f(-1)$，$b=\dfrac 12f(1)+\dfrac 12f(-1)-1$，从而$$a-3b=-f(1)-2f(-1)+3\geqslant -1-2+3=0,$$等号当 $f(x)=x^2$ 时可以取得．
综上所述，$a-3b$ 当 $a=\dfrac 23$，$b=-\dfrac 89$ 时取得最大值为 $\dfrac{10}3$；当 $a=b=0$ 时取得最小值为 $0$．结合连续性，$a-3b$ 的取值范围为 $\left[0,\dfrac{10}3\right]$．