已知单位向量 $\overrightarrow a,\overrightarrow b,\overrightarrow c,\overrightarrow x$,且 $\overrightarrow a+\overrightarrow b+\overrightarrow c=\overrightarrow 0$,设$$y=\Big|\overrightarrow a-\overrightarrow x\Big|+\Big|\overrightarrow b-\overrightarrow x\Big|+\Big|\overrightarrow c-\overrightarrow x\Big|,$$则 $y$ 的最大值是 .
【难度】
【出处】
无
【标注】
【答案】
$3\sqrt 2$
【解析】
由柯西不等式,有\begin{eqnarray*}\begin{split} y&=\Big|\overrightarrow a-\overrightarrow x\Big|+\Big|\overrightarrow b-\overrightarrow x\Big|+\Big|\overrightarrow c-\overrightarrow x\Big|\\
&\leqslant \sqrt 3\cdot \sqrt{\left(\overrightarrow a-\overrightarrow x\right)^2+\left(\overrightarrow b-\overrightarrow x\right)^2+\left(\overrightarrow c-\overrightarrow x\right)^2}\\
&=\sqrt 3\cdot \sqrt{\overrightarrow a^2+\overrightarrow b^2+\overrightarrow c^2+3\overrightarrow x^2-2\overrightarrow x\cdot \left(\overrightarrow a+\overrightarrow b+\overrightarrow c\right)}\\
&=3\sqrt 2
,\end{split} \end{eqnarray*}等号当 $\Big|\overrightarrow a-\overrightarrow x\Big|=\Big|\overrightarrow b-\overrightarrow x\Big|=\Big|\overrightarrow c-\overrightarrow x\Big|$ 时取得.
事实上,有 $\overrightarrow a=-\left(\overrightarrow b+\overrightarrow c\right)$,于是可得$$\overrightarrow a^2=\left(\overrightarrow b+\overrightarrow c\right)^2,$$因此 $\overrightarrow b\cdot \overrightarrow c=-\dfrac 12$,类似的,可得$$\overrightarrow a\cdot \overrightarrow b=\overrightarrow b\cdot \overrightarrow c=\overrightarrow c\cdot \overrightarrow a=-\dfrac 12.$$因此 $\overrightarrow a,\overrightarrow b,\overrightarrow c$ 是共面向量,且两两的夹角均为 $120^\circ$.进而取 $\overrightarrow x$ 与 $\overrightarrow a,\overrightarrow b,\overrightarrow c$ 均垂直,即可取得等号.因此所求的最大值为 $3\sqrt 2$.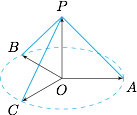
&\leqslant \sqrt 3\cdot \sqrt{\left(\overrightarrow a-\overrightarrow x\right)^2+\left(\overrightarrow b-\overrightarrow x\right)^2+\left(\overrightarrow c-\overrightarrow x\right)^2}\\
&=\sqrt 3\cdot \sqrt{\overrightarrow a^2+\overrightarrow b^2+\overrightarrow c^2+3\overrightarrow x^2-2\overrightarrow x\cdot \left(\overrightarrow a+\overrightarrow b+\overrightarrow c\right)}\\
&=3\sqrt 2
,\end{split} \end{eqnarray*}等号当 $\Big|\overrightarrow a-\overrightarrow x\Big|=\Big|\overrightarrow b-\overrightarrow x\Big|=\Big|\overrightarrow c-\overrightarrow x\Big|$ 时取得.
事实上,有 $\overrightarrow a=-\left(\overrightarrow b+\overrightarrow c\right)$,于是可得$$\overrightarrow a^2=\left(\overrightarrow b+\overrightarrow c\right)^2,$$因此 $\overrightarrow b\cdot \overrightarrow c=-\dfrac 12$,类似的,可得$$\overrightarrow a\cdot \overrightarrow b=\overrightarrow b\cdot \overrightarrow c=\overrightarrow c\cdot \overrightarrow a=-\dfrac 12.$$因此 $\overrightarrow a,\overrightarrow b,\overrightarrow c$ 是共面向量,且两两的夹角均为 $120^\circ$.进而取 $\overrightarrow x$ 与 $\overrightarrow a,\overrightarrow b,\overrightarrow c$ 均垂直,即可取得等号.因此所求的最大值为 $3\sqrt 2$.

题目
答案
解析
备注