若直线 $l$ 与曲线 $C$ 满足下列两个条件:
(i)直线 $l$ 在点 $P\left({x_0},{y_0}\right)$ 处与曲线 $C$ 相切;
(ii)曲线 $C$ 在点 $P$ 附近位于直线 $l$ 的两侧,则称直线 $l$ 在点 $P$ 处"切过"曲线 $C$.
下列命题正确的是 .(写出所有正确命题的编号)
① 直线 $l:y = 0$ 在点 $P\left({0,0}\right)$ 处"切过"曲线 $C:y ={x^3}$;
② 直线 $l:x = - 1$ 在点 $P\left({ - 1,0}\right)$ 处"切过"曲线 $C:y ={\left(x + 1\right)^3}$;
③ 直线 $l:y = x$ 在点 $P\left({0,0}\right)$ 处"切过"曲线 $C:y = \sin x$;
④ 直线 $l:y = x$ 在点 $P\left({0,0}\right)$ 处"切过"曲线 $C:y = \tan x$;
⑤ 直线 $l:y = x - 1$ 在点 $P\left({1,0}\right)$ 处"切过"曲线 $C:y = \ln x$.
(i)直线 $l$ 在点 $P\left({x_0},{y_0}\right)$ 处与曲线 $C$ 相切;
(ii)曲线 $C$ 在点 $P$ 附近位于直线 $l$ 的两侧,则称直线 $l$ 在点 $P$ 处"切过"曲线 $C$.
下列命题正确的是
① 直线 $l:y = 0$ 在点 $P\left({0,0}\right)$ 处"切过"曲线 $C:y ={x^3}$;
② 直线 $l:x = - 1$ 在点 $P\left({ - 1,0}\right)$ 处"切过"曲线 $C:y ={\left(x + 1\right)^3}$;
③ 直线 $l:y = x$ 在点 $P\left({0,0}\right)$ 处"切过"曲线 $C:y = \sin x$;
④ 直线 $l:y = x$ 在点 $P\left({0,0}\right)$ 处"切过"曲线 $C:y = \tan x$;
⑤ 直线 $l:y = x - 1$ 在点 $P\left({1,0}\right)$ 处"切过"曲线 $C:y = \ln x$.
【难度】
【出处】
2014年高考安徽卷(文)
【标注】
【答案】
①③④
【解析】
注意比较在 $x_0$ 附近函数图象与切线的位置关系即可.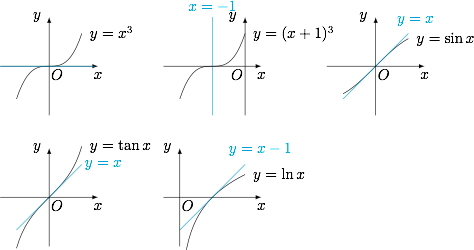

题目
答案
解析
备注