设实数 $x,y,z$ 满足$$\begin{cases} |x+2y-3z|\leqslant 6,\\ |x-2y+3z|\leqslant 6,\\ |x-2y-3z|\leqslant 6,\\ |x+2y+3z|\leqslant 6,\end{cases}$$则 $|x|+|y|+|z|$ 的最大值为 ．
【难度】
【出处】
无
【标注】
【答案】
$6$
【解析】
把 $z$ 看成参数，有$$\begin{cases} 3z-6\leqslant x+2y\leqslant 3z+6,\\ -3z-6\leqslant x-2y\leqslant -3z+6,\\ 3z-6\leqslant x-2y\leqslant 3z+6,\\ -3z-6\leqslant x+2y\leqslant -3z+6,\end{cases}$$根据对称性，不妨设 $z\geqslant 0$．于是条件简化为$$\begin{cases} 3z-6\leqslant x+2y\leqslant -3z+6,\\ 3z-6 \leqslant x-2y\leqslant -3z+6,\end{cases}$$该不等式组有解即 $z\in [0,2]$，表示一个菱形及其内部（$z=2$ 时退化为一个点），如图．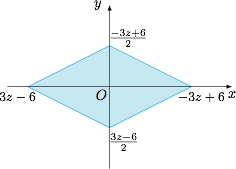
于是可得$$|x|+|y|+|z|\leqslant 6-3z+z=6-2z\leqslant 6,$$等号当 $x=6$，$y=0$，$z=0$ 时取得．于是所求的最大值为 $6$．
于是可得$$|x|+|y|+|z|\leqslant 6-3z+z=6-2z\leqslant 6,$$等号当 $x=6$，$y=0$，$z=0$ 时取得．于是所求的最大值为 $6$．
题目
答案
解析
备注
