曲线 $C$ 是平面内到定点 $A(1,0)$ 的距离与到定直线的距离 $x=-1$ 的距离之和为 $3$ 的动点 $P$ 的轨迹,则曲线 $C$ 与 $y$ 轴的交点的横坐标是 ;又已知 $B(a,1)$($a$ 为参数),那么 $|PA|+|PB|$ 的最小值 $d(a)=$ .
【难度】
【出处】
无
【标注】
【答案】
$\left(0,\pm \sqrt 3\right)$,$\begin{cases} \sqrt{a^2-2a+2},&a<-\dfrac 75,\\ a+4,&-\dfrac 75\leqslant a\leqslant -1,\\ 2-a,&-1<a\leqslant 1,\\ \sqrt{a^2-2a+2},&a>1.\end{cases}$
【解析】
作与直线 $x=-1$ 的距离为 $3$ 的两条直线 $x=2$,$x=-4$,那么“到定点与定直线 $x=-1$ 的距离之和为 $3$”,就转化成了“在直线 $x=-1$ 的左侧到定点的距离与到直线 $x=-4$ 的距离相等,或在直线 $x=-1$ 的右侧到定点的距离与到直线 $x=2$ 的距离相等”,如左图.曲线 $C$ 由抛物线弧 $y^2=-2\left(x-\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$ 和抛物线弧 $y^2=10\left(x+\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$ 共同组成.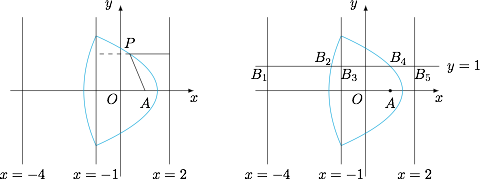 容易求出曲线 $C$ 与 $y$ 轴的交点坐标为 $\left(0,\pm\sqrt 3\right)$.接下来研究对于 $B(a,1)$,$|PB|+|PA|$ 的最小值 $d(a)$.如右图,设直线 $y=1$ 与直线 $x=-4$,抛物线弧 $y^2=10\left(x+\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$,直线 $x=-1$,抛物线弧 $y^2=-2\left(x-\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$,直线 $x=2$ 依次交于 $B_1\left(-4,1\right)$,$B_2\left(-\dfrac 75,1\right)$,$B_3\left(-1,1\right)$,$B_4\left(1,1\right)$,$B_5\left(2,1\right)$.以 $B_1,B_2,B_3,B_4,B_5$ 为分界点分类讨论,可得$$d(a)=\begin{cases} \sqrt{a^2-2a+2},&a<-\dfrac 75,\\ a+4,&-\dfrac 75\leqslant a\leqslant -1,\\ 2-a,&-1<a\leqslant 1,\\ \sqrt{a^2-2a+2},&a>1.\end{cases}$$
容易求出曲线 $C$ 与 $y$ 轴的交点坐标为 $\left(0,\pm\sqrt 3\right)$.接下来研究对于 $B(a,1)$,$|PB|+|PA|$ 的最小值 $d(a)$.如右图,设直线 $y=1$ 与直线 $x=-4$,抛物线弧 $y^2=10\left(x+\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$,直线 $x=-1$,抛物线弧 $y^2=-2\left(x-\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$,直线 $x=2$ 依次交于 $B_1\left(-4,1\right)$,$B_2\left(-\dfrac 75,1\right)$,$B_3\left(-1,1\right)$,$B_4\left(1,1\right)$,$B_5\left(2,1\right)$.以 $B_1,B_2,B_3,B_4,B_5$ 为分界点分类讨论,可得$$d(a)=\begin{cases} \sqrt{a^2-2a+2},&a<-\dfrac 75,\\ a+4,&-\dfrac 75\leqslant a\leqslant -1,\\ 2-a,&-1<a\leqslant 1,\\ \sqrt{a^2-2a+2},&a>1.\end{cases}$$
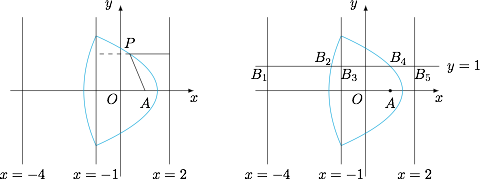 容易求出曲线 $C$ 与 $y$ 轴的交点坐标为 $\left(0,\pm\sqrt 3\right)$.接下来研究对于 $B(a,1)$,$|PB|+|PA|$ 的最小值 $d(a)$.如右图,设直线 $y=1$ 与直线 $x=-4$,抛物线弧 $y^2=10\left(x+\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$,直线 $x=-1$,抛物线弧 $y^2=-2\left(x-\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$,直线 $x=2$ 依次交于 $B_1\left(-4,1\right)$,$B_2\left(-\dfrac 75,1\right)$,$B_3\left(-1,1\right)$,$B_4\left(1,1\right)$,$B_5\left(2,1\right)$.以 $B_1,B_2,B_3,B_4,B_5$ 为分界点分类讨论,可得$$d(a)=\begin{cases} \sqrt{a^2-2a+2},&a<-\dfrac 75,\\ a+4,&-\dfrac 75\leqslant a\leqslant -1,\\ 2-a,&-1<a\leqslant 1,\\ \sqrt{a^2-2a+2},&a>1.\end{cases}$$
容易求出曲线 $C$ 与 $y$ 轴的交点坐标为 $\left(0,\pm\sqrt 3\right)$.接下来研究对于 $B(a,1)$,$|PB|+|PA|$ 的最小值 $d(a)$.如右图,设直线 $y=1$ 与直线 $x=-4$,抛物线弧 $y^2=10\left(x+\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$,直线 $x=-1$,抛物线弧 $y^2=-2\left(x-\dfrac 32\right),y\in\left[-\sqrt 5,\sqrt 5\right]$,直线 $x=2$ 依次交于 $B_1\left(-4,1\right)$,$B_2\left(-\dfrac 75,1\right)$,$B_3\left(-1,1\right)$,$B_4\left(1,1\right)$,$B_5\left(2,1\right)$.以 $B_1,B_2,B_3,B_4,B_5$ 为分界点分类讨论,可得$$d(a)=\begin{cases} \sqrt{a^2-2a+2},&a<-\dfrac 75,\\ a+4,&-\dfrac 75\leqslant a\leqslant -1,\\ 2-a,&-1<a\leqslant 1,\\ \sqrt{a^2-2a+2},&a>1.\end{cases}$$
题目
答案
解析
备注