考虑反面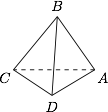：法一以 $B,C$ 与 $B,D$ 是否连边分情况讨论．
① 若 $B,C$ 与 $B,D$ 都不连边，则一定满足情况，所求概率为$$\dfrac 12\times\dfrac 12\times\dfrac 12=\dfrac 18;$$② 若 $B,C$ 与 $B,D$ 都连边，那么 $A,C$ 与 $A,D$ 都不连边，所求概率为$$\left(\dfrac 12\right)^5=\dfrac 1{32};$$③ 若 $B,C$ 与 $B,D$ 恰有一组连边，不妨考虑 $B,C$ 连边，$B,D$ 不连边，则 $A,C$ 不连边，且 $C,D$ 与 $A,D$ 不同时连边即可，所求概率为$$\dfrac 12\times\dfrac 12\times\dfrac 12\times \dfrac 12\times\left(1-\dfrac 14\right)=\dfrac {3}{64}.$$所以 $A,B$ 不能用空间折线连接的概率为$$\dfrac 18+\dfrac 1{32}+2\times\dfrac {3}{64}=\dfrac 14.$$从而所求概率为 $1-\dfrac 14=\dfrac 34$．
法二按 $C,D$ 是否连边分两种情况讨论：
① 若 $C,D$ 不连边，则满足条件的有三种情况：$A,D$，$B,D$，$A,C$ 与 $B,C$ 都不连边；仅有一组连边；或有两组连边，但 $A,D$ 与 $B,D$ 不同时连边，$A,C$ 与 $B,C$ 不同时连边均可．
故所求概率为$$\dfrac 12\times\dfrac 12\times\left[\left(\dfrac 12\right)^4+{\rm C}_4^1\times\left(\dfrac 12\right)^4+{\rm C}_2^1\times{\rm C}_2^1\times\left(\dfrac 12\right)^4\right]=\dfrac 9{64}.$$② 若 $C,D$ 连边，也有三种情况：$A,D$，$B,D$，$A,C$，$B,C$ 全不连边；或只有一组连边，或有两组连边，但两组连边为 $AD,AC$ 或 $BC,BD$．
所求概率为$$\dfrac 12\times\dfrac 12\times\left[\dfrac {1}{16}+{\rm C}_4^3\times\left(\dfrac 12\right)^4+2\times\left(\dfrac 12\right)^4\right]=\dfrac {7}{64}.$$从而 $A,B$ 不能用折线连接的概率为$$\dfrac 9{64}+\dfrac 7{64}=\dfrac 14,$$所求概率为 $1-\dfrac 14=\dfrac 34$．