已知函数 $f(x)=x^2+2x+1$，若存在实数 $t$，当 $x\in [1,m]$ 时，$f(x+t)\leqslant x$ 恒成立，则实数 $m$ 的最大值为 ．
【难度】
【出处】
无
【标注】
【答案】
$4$
【解析】
根据题意，参数 $t$ 控制抛物线 $y=x^2$ 的左右平移，如图：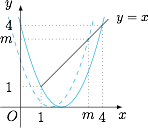
当点 $(1,1)$ 在函数 $y=f(x+t)$ 的图象上时，解得 $t=-3$，再通过 $(x-2)^2=x$ 就可以得到 $m=4$．
从严格的代数计算角度来说，由必要条件$$\begin{cases} f(1+t)\leqslant 1,\\f(m+t)\leqslant 1,\end{cases}$$得到$$\begin{cases} -3\leqslant t\leqslant -1,\\-\sqrt m-m-1\leqslant t\leqslant \sqrt m-m-1,\end{cases}$$因为 $m>1$，所以有 $\sqrt m-m-1<-1$，从而当 $\sqrt m-m-1\geqslant -3$ 时，$t$ 存在，解得 $m\leqslant 4$．
当点 $(1,1)$ 在函数 $y=f(x+t)$ 的图象上时，解得 $t=-3$，再通过 $(x-2)^2=x$ 就可以得到 $m=4$．从严格的代数计算角度来说，由必要条件$$\begin{cases} f(1+t)\leqslant 1,\\f(m+t)\leqslant 1,\end{cases}$$得到$$\begin{cases} -3\leqslant t\leqslant -1,\\-\sqrt m-m-1\leqslant t\leqslant \sqrt m-m-1,\end{cases}$$因为 $m>1$，所以有 $\sqrt m-m-1<-1$，从而当 $\sqrt m-m-1\geqslant -3$ 时，$t$ 存在，解得 $m\leqslant 4$．
题目
答案
解析
备注
