已知等比数列 $a_1,a_2,a_3,a_4$ 满足 $a_1\in (0,1)$，$a_2\in (1,2)$，$a_3\in (2,3)$，则 $a_4$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left(2^{\frac 32},9\right)$
【解析】
根据题意，等比数列的首项和公比均为正数，设 $x=\ln a_1$，$y=\ln \dfrac{a_2}{a_1}$，则$$\begin{cases} x<0,\\ 0<x+y<\ln 2,\\ \ln 2<x+2y< \ln 3,\end{cases}$$求 ${\rm e}^{x+3y}$ 的取值范围，这是一个典型的线性规划问题，可行域如图．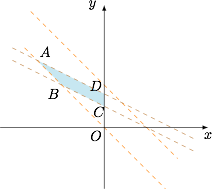
容易求得 $A\left(-\ln 3,\ln 3\right)$，$B\left(-\ln 2,\ln 2\right)$，$C\left(0,\dfrac 12\ln 2\right)$，$D\left(0,\dfrac 12\ln 3\right)$，因此不难得到$$\dfrac 32\ln 2<x+3y<2\ln 3,$$因此所求的取值范围是 $\left(2^{\frac 32},9\right)$．
容易求得 $A\left(-\ln 3,\ln 3\right)$，$B\left(-\ln 2,\ln 2\right)$，$C\left(0,\dfrac 12\ln 2\right)$，$D\left(0,\dfrac 12\ln 3\right)$，因此不难得到$$\dfrac 32\ln 2<x+3y<2\ln 3,$$因此所求的取值范围是 $\left(2^{\frac 32},9\right)$．
题目
答案
解析
备注
