已知函数 $f(x)=ax^2+4x-2$，当实数 $a$ 变化时，有 $\forall x\in [m,0],|f(x)|\leqslant 4$，则 $m$ 的最小值是 ，此时 $a$ 的值是 ．
【难度】
【出处】
无
【标注】
【答案】
$-3$，$2$
【解析】
先猜到取最小值的情形，如图，有$$\dfrac{4a\cdot(-2)-16}{4a}=-4,$$解得 $a=2$，从而得到 $m=-3$．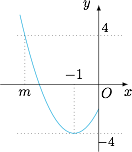
下面证明 $-3$ 为 $m$ 的最小值：
若 $a=0$，容易求得 $m$ 的最小值为 $-\dfrac 12$；
若 $a<0$，则 $f(x)$ 在 $[m,0]$ 上单调递增，因为 $f(-1)=a-6<-6<-4$，所以 $m>-1>-3$；
若 $a>0$，存在 $a$ 使得 $m<-3$，则根据题意有$$\begin{cases} f(-1)=a-6>-4,\\f(-3)=9a-14<4,\end{cases}$$解得 $2<a<2$，无解，所以 $m\geqslant -3$．由上面的函数知，$-3$ 可以取到，所以 $-3$ 是所求的 $m$ 的最小值．
下面证明 $-3$ 为 $m$ 的最小值：若 $a=0$，容易求得 $m$ 的最小值为 $-\dfrac 12$；
若 $a<0$，则 $f(x)$ 在 $[m,0]$ 上单调递增，因为 $f(-1)=a-6<-6<-4$，所以 $m>-1>-3$；
若 $a>0$，存在 $a$ 使得 $m<-3$，则根据题意有$$\begin{cases} f(-1)=a-6>-4,\\f(-3)=9a-14<4,\end{cases}$$解得 $2<a<2$，无解，所以 $m\geqslant -3$．由上面的函数知，$-3$ 可以取到，所以 $-3$ 是所求的 $m$ 的最小值．
题目
答案
解析
备注
