已知点 $P$ 是圆 $O:x^2+y^2=1$ 上一动点，$O$ 为坐标原点．过点 $P$ 作圆 $O$ 的切线 $l$ 与圆 $O_1:x^2+y^2-2x-8y=19$ 相交于 $A,B$ 两点，则 $\dfrac{AP}{BP}$ 的最大值为 ．
【难度】
【出处】
无
【标注】
【答案】
$3+2\sqrt 2$
【解析】
不改变问题的本质，将问题拓展．已知单位圆 $O:x^2+y^2=1$ 及其在 $P(0,1)$ 处的切线 $l:y=1$，圆 $O_1$ 的圆心到 $O$ 的距离为 $d$，半径为 $r$ 且与直线 $l$ 交于 $A,B$ 两点，求 $A,B$ 两点横坐标的绝对值的比的取值范围．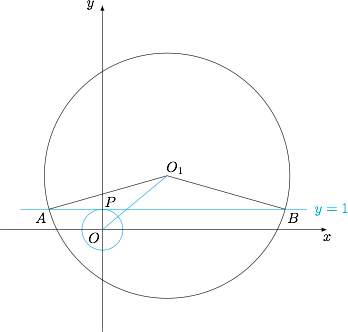
设 $O_1(d\cos\theta,d\sin\theta)$，则圆 $O_1$ 的方程为$$(x-d\cos\theta)^2+(y-d\sin\theta)^2=r^2,$$与直线 $l$ 的方程联立可得$$x^2-2d\cos\theta\cdot x+d^2-r^2-2d\sin\theta+1=0.$$设 $A,B$ 两点横坐标的比为 $\lambda$，则$$\left(-2d\cos\theta\right)^2=\left(\lambda+\dfrac{1}{\lambda}+2\right)\left(d^2-r^2-2d\sin\theta+1\right),$$整理得$$\lambda+\dfrac{1}{\lambda}=m+2d\sin\theta+\dfrac{m^2-4d^2}{m+2d\sin\theta}-2m-2,$$其中 $m=r^2-d^2-1$．
当 $m^2-4d^2\geqslant 0$ 时，$\lambda+\dfrac{1}{\lambda}$ 的取值范围是 $\left[2\sqrt{m^2-4d^2}-2m-2,-2\right]$，最小值当 $m+2d\sin\theta=\sqrt{m^2-4d^2}$ 时取得，最大值当 $\sin\theta=\pm 1$ 时取得．
回到本题中，有 $m=r^2-d^2-1=18$，于是 $\lambda+\dfrac{1}{\lambda}$ 的最小值为 $-6$，进而可得 $\dfrac{AP}{BP}$ 的最大值为 $3+2\sqrt 2$．
设 $O_1(d\cos\theta,d\sin\theta)$，则圆 $O_1$ 的方程为$$(x-d\cos\theta)^2+(y-d\sin\theta)^2=r^2,$$与直线 $l$ 的方程联立可得$$x^2-2d\cos\theta\cdot x+d^2-r^2-2d\sin\theta+1=0.$$设 $A,B$ 两点横坐标的比为 $\lambda$，则$$\left(-2d\cos\theta\right)^2=\left(\lambda+\dfrac{1}{\lambda}+2\right)\left(d^2-r^2-2d\sin\theta+1\right),$$整理得$$\lambda+\dfrac{1}{\lambda}=m+2d\sin\theta+\dfrac{m^2-4d^2}{m+2d\sin\theta}-2m-2,$$其中 $m=r^2-d^2-1$．当 $m^2-4d^2\geqslant 0$ 时，$\lambda+\dfrac{1}{\lambda}$ 的取值范围是 $\left[2\sqrt{m^2-4d^2}-2m-2,-2\right]$，最小值当 $m+2d\sin\theta=\sqrt{m^2-4d^2}$ 时取得，最大值当 $\sin\theta=\pm 1$ 时取得．
回到本题中，有 $m=r^2-d^2-1=18$，于是 $\lambda+\dfrac{1}{\lambda}$ 的最小值为 $-6$，进而可得 $\dfrac{AP}{BP}$ 的最大值为 $3+2\sqrt 2$．
题目
答案
解析
备注
