已知函数 $f(x)={\rm e}^x\left(2-{\rm e}^x\right)+(a+2)\left|{\rm e}^x-1\right|-a^2$ 的零点个数为 $3$,则实数 $a$ 的取值范围是 .
【难度】
【出处】
无
【标注】
【答案】
$(1,2)$
【解析】
设 $t={\rm e}^x$,且\[\varphi(t)=t(2-t)+(a+2)\cdot |t-1|-a^2,\]根据题意,$\varphi(t)$ 在 $t\in\left(0,+\infty\right)$ 上有 $3$ 个零点.由于 $\varphi(t)$ 的图象为“m”形,且对称轴为 $t=1$,于是必然有\[\begin{cases}\varphi(0)>0,\\ \varphi(1)<0,\end{cases}\]即\[\begin{cases}a+2-a^2>0,\\ 1-a^2<0,\end{cases}\]解得 $a$ 的取值范围是 $(1,2)$.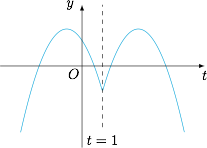

题目
答案
解析
备注