查看数据源：59101c29857b42000aca396a
已知 $f(x) =\begin{cases}\lg \left( x + 1 \right) + 1 ,x \geqslant 0\\\lg \left( 1 - x \right) + 1 ,x < 0 \end{cases}$，若不等式 $f\left( {ax - 1} \right) > f\left( {x - 2} \right)$ 在 $\left[ {3,4} \right]$ 上有解，则实数 $a$ 的取值范围为 ．
【难度】
【出处】
2011年南京理工大学自主招生暨保送生考试数学试题
【标注】
  • 知识点
    >
    不等式
    >
    解不等式
    >
    解函数不等式
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的对称性
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的单调性
【答案】
$\left(-\infty,0\right)\cup\left(\dfrac 23,+\infty\right)$
【解析】
如图，$f(x)$ 是偶函数，且在 $[0,+\infty)$ 上单调递增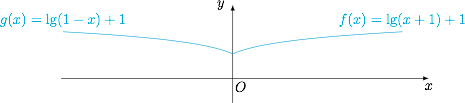：所以$$f\left( {ax - 1} \right) > f\left( {x - 2} \right) \Leftrightarrow \left| {ax - 1} \right| > \left| {x - 2} \right|.$$从而不等式 $f\left( {ax - 1} \right) > f\left( {x - 2} \right)$ 在 $\left[3,4\right]$ 上有解当且仅当存在 $x\in [3,4]$，使得$$ \left| {ax - 1} \right| > \left| {x - 2} \right| \Leftrightarrow \left| {ax - 1} \right| > x - 2.$$所以$$\begin{cases}ax - 1 > x - 2 \\ 3 \leqslant x \leqslant 4 \end{cases}\lor\begin{cases}ax - 1 < 2 - x \\3 \leqslant x \leqslant 4 \end{cases}$$有解，即$$\begin{cases}\left( {a - 1} \right)x + 1 > 0\\3 \leqslant x \leqslant 4 \end{cases}\lor\begin{cases} \left( {a + 1} \right)x - 3 < 0 \\ 3 \leqslant x \leqslant 4 \\ \end{cases}$$有解，也即$$3\left( {a - 1} \right) + 1 > 0\lor 4\left( {a - 1} \right) + 1 > 0\lor 3\left( {a + 1} \right) - 3 < 0\lor 4\left( {a + 1} \right) - 3 < 0$$有解，所以$$ a > \dfrac{2}{3}\lor a > \dfrac{3}{4}\lor a < 0\lor a <- \dfrac{1}{4}.$$因此 $ a < 0$ 或 $a > \dfrac{2}{3}$．
题目 答案 解析 备注
0.110039s