有三支股票A、B、C，$28$ 位股民的持有情况如下：每位股民至少持有其中一支股票．在不持有A股票的人中，持有B股票的人数是持有C股票人数的 $2$ 倍．在持有A股票的人中，只持有A股票的人数比除了持有A股票外，同时还持有其他股票的人数多 $1$．在只持有一支股票的人中，有一半持有A股票．则只持有B股票的股民人数是 ．
【难度】
【出处】
无
【标注】
【答案】
$7$
【解析】
如图，设每个区域的股民人数分别为 $a,b,c,x,y,z,m$．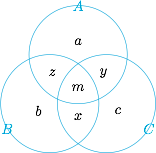
根据题意有\[\begin{cases} a+b+c+x+y+z+m=28,\\ b+x=2(c+x),\\ a=y+z+m+1,\\ a=b+c,
\end{cases}\]将 $y+z+m$ 看成一个整体，可得\[\begin{cases}a=29-3b,\\
c=29-4b,\\
x=9b-58,\\
y+z+m=28-3b,\\
\end{cases}\]由于 $c\geqslant 1$，且 $x\geqslant 0$，于是 $b=7$，进而\[(a,b,c,x,y+z+m)=(8,7,1,5,7).\]
根据题意有\[\begin{cases} a+b+c+x+y+z+m=28,\\ b+x=2(c+x),\\ a=y+z+m+1,\\ a=b+c,\end{cases}\]将 $y+z+m$ 看成一个整体，可得\[\begin{cases}a=29-3b,\\
c=29-4b,\\
x=9b-58,\\
y+z+m=28-3b,\\
\end{cases}\]由于 $c\geqslant 1$，且 $x\geqslant 0$，于是 $b=7$，进而\[(a,b,c,x,y+z+m)=(8,7,1,5,7).\]
题目
答案
解析
备注
