查看数据源：60c0600195a31e000a975f9e
已知 $O$ 为坐标原点，点 $P_1(\cos \alpha,\sin \alpha)$，$P_2(\cos \beta, -\sin \beta)$，$P_3(\cos(\alpha + \beta),sin(\alpha + \beta))$，$A(1, 0)$，则  \((\qquad)\)
A: $|\overrightarrow{OP_1}|=|\overrightarrow{OP_2}|$
B: $|\overrightarrow{AP_1}|=|\overrightarrow{AP_2}|$
C: $\overrightarrow{OA}\cdot\overrightarrow{OP_3}=\overrightarrow{OP_1}\cdot\overrightarrow{OP_2}$
D: $\overrightarrow{OA}\cdot\overrightarrow{OP_1}=\overrightarrow{OP_2}\cdot\overrightarrow{OP_3}$
【难度】
【出处】
无
【标注】
【答案】
AC
【解析】
如图，可知 $A.|OP_1|=|OP_2|=1$ $B.$ 只有 $\alpha=-\beta$ 时成立 $C.<\overrightarrow{OA},\overrightarrow{OP_3}>=\alpha+\beta$，$<\overrightarrow{OP_1},\overrightarrow{OP_2}>=\alpha+\beta$，故正确．$D.$ 错误．故选 $AC$\begin{center} \end{center}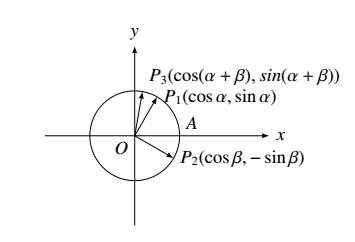
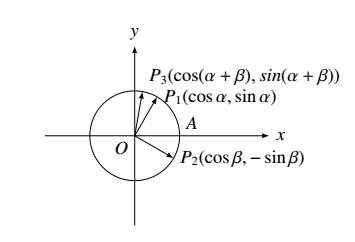
题目 答案 解析 备注
0.166795s