已知 $P$ 为椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 上位于第一象限内的点,$F_1,F_2$ 为椭圆的左、右焦点,则 $\angle F_1PF_2$ 的角平分线与 $y$ 轴公共点的纵坐标 $t$ 的取值范围是 .
【难度】
【出处】
无
【标注】
【答案】
$\left(-\dfrac {c^2}{b},0\right)$
【解析】
设 $P(m,n)$,$m,n>0$,则点 $P$ 处的切线斜率 $k=-\dfrac{b^2m}{a^2n}$,根据椭圆的光学性质,可得角平分线的斜率为 $\dfrac{a^2n}{b^2m}$,于是有\[\dfrac{n-t}{m-0}=\dfrac{a^2n}{b^2m},\]于是\[t=-\dfrac{c^2}{b^2}\cdot n,\]其中 $c$ 为椭圆的半焦距.考虑到 $n$ 的取值范围是 $(0,b)$,于是 $t$ 的取值范围是 $\left(-\dfrac{c^2}b,0\right)$.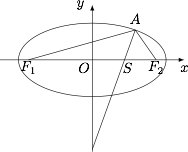

题目
答案
解析
备注