若 $\alpha\in \left(0,\frac{\pi}{2}\right), \tan2\alpha=\frac{\cos\alpha}{2-\sin\alpha}$,则 $\tan\alpha=$ \((\qquad)\) .
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
$\tan 2\alpha=\frac{\cos\alpha}{2-\sin\alpha}$.
$\tan2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}=\frac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}=\frac{\cos\alpha}{2-\sin\alpha}$.
所以 $2\sin\alpha(2-\sin\alpha)=\cos^2\alpha-\sin^2\alpha$
所以 $4\sin\alpha-2\sin^2\alpha=\cos^2\alpha-\sin^2\alpha=1-2\sin^2\alpha$
所以 $\sin\alpha=\frac{1}{4}$.
又因为 $\alpha\in\left(0,\frac{\pi}{2}\right)$.如图,$\tan\alpha=\frac{1}{\sqrt{15}}=\frac{\sqrt{15}}{15}$.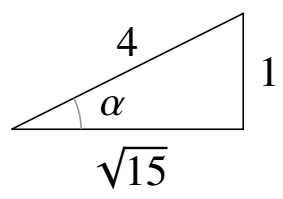
$\tan2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}=\frac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}=\frac{\cos\alpha}{2-\sin\alpha}$.
所以 $2\sin\alpha(2-\sin\alpha)=\cos^2\alpha-\sin^2\alpha$
所以 $4\sin\alpha-2\sin^2\alpha=\cos^2\alpha-\sin^2\alpha=1-2\sin^2\alpha$
所以 $\sin\alpha=\frac{1}{4}$.
又因为 $\alpha\in\left(0,\frac{\pi}{2}\right)$.如图,$\tan\alpha=\frac{1}{\sqrt{15}}=\frac{\sqrt{15}}{15}$.

题目
答案
解析
备注