平面直角坐标系 $xOy$ 中,双曲线 $C_1:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\left(a>0,b>0\right)$ 的渐近线与抛物线 $C_2:x^2=2py\left(p>0\right)$ 交于 $O$,$A$,$B$.若 $\triangle OAB$ 的垂心为 $C_2$ 的焦点,则 $C_1$ 的离心率为 .
【难度】
【出处】
无
【标注】
【答案】
$\dfrac 32$
【解析】
联立抛物线与双曲线方程,可得到 $A$,$B$ 的坐标,又 $\triangle OAB$ 的垂心是 $C_2$ 的焦点 $F$,故 $BF\perp AO$,由向量数量积为 $0$,可得到 $a$,$b$ 的关系,结合 $c^2=a^2+b^2$,从而确定离心率 $e$.此题属于圆锥曲线中确定基本量的问题.双曲线的渐近线为 $y=\pm \dfrac{b}{a}x$,将双曲线与渐近线方程联立可求得 $A$,$B$ 坐标分别为 $A\left(\dfrac {2pb}a,\dfrac {2pb^2}{a^2}\right)$,$B\left(-\dfrac {2pb}a,\dfrac {2pb^2}{a^2}\right)$,而抛物线 $C_2$ 的焦点为 $F\left(0,\dfrac p2\right)$,由 $BF\perp OA$ 可得 $4b^2=5a^2$,进而可得 $C_1$ 的离心率为 $\dfrac ca=\dfrac 32$.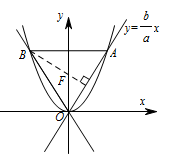

题目
答案
解析
备注