已知点 $P$ 在圆 $(x - 5)^2 + (y - 5)^2 = 16$ 上，点 $A(4, 0)$，$B(0, 2)$，则 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
ACD
【解析】
如图 $1$ 所示，记条件中圆为 $\odot M$，点 $P$ 到直线 $AB$ 的距离 $d$ 满足：$P_1H\leqslant d\leqslant P_2H$ 又 $l_{AB}:x+y-4=0$，所以 $MH=\frac{|5+2\times5-4|}{\sqrt{1^2+2^2}}=\frac{11}{\sqrt{5}}$，$P_1H=\frac{11}{\sqrt{5}}-4$，$P_2H=\frac{11}{\sqrt{5}}+4$，$d\in[\frac{11}{\sqrt{5}}-4, \frac{11}{\sqrt{5}}+4]$ 又 $\frac{11}{\sqrt{5}}-4<2$，$\frac{11}{\sqrt{5}}+4<10$，所以 $A$ 正确，$B$ 错误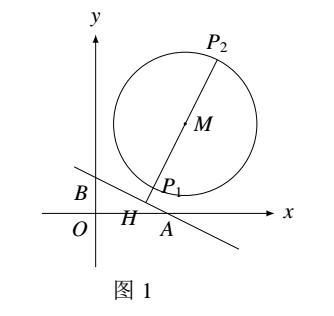．\begin{center} \end{center}
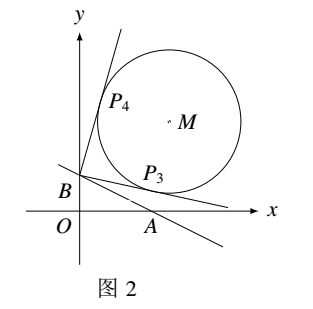
如图 $2$ 所示，点 $P$ 在 $\odot M$ 上，作 $BP_3$，$BP_4$ 切 $\odot M$ 于点 $P_3$，$P_4$，则 $\angle PBA$ 在 $P_3$ 处最小，$P_4$ 处最大．又 $BP_3=BP_4=\sqrt{BP^2-4^2}=\sqrt{5^2+(5-2)^2-4^2}=3\sqrt{2}$．所以 $CD$ 正确．\begin{center} \end{center}
如图 $2$ 所示，点 $P$ 在 $\odot M$ 上，作 $BP_3$，$BP_4$ 切 $\odot M$ 于点 $P_3$，$P_4$，则 $\angle PBA$ 在 $P_3$ 处最小，$P_4$ 处最大．又 $BP_3=BP_4=\sqrt{BP^2-4^2}=\sqrt{5^2+(5-2)^2-4^2}=3\sqrt{2}$．所以 $CD$ 正确．\begin{center} \end{center}
题目
答案
解析
备注
