如图，$AB$ 为圆 $O$ 的直径，$E$ 为 $AB$ 延长线上一点，过 $E$ 作圆 $O$ 的切线，切点为 $C$，过 $A$ 作直线 $EC$ 的垂线，垂足为 $D$．若 $AB=4$，$CE=2\sqrt 3$，则 $AD=$ ．
【难度】
【出处】
2015年高考广东卷（文）
【标注】
【答案】
$ 3 $
【解析】
本小题考查了切割线定理以及平行截割定理．条件给出切线长，有割线，故可用切割线定理建立等式关系，再有相似比得到结果．连接 $OC$，如图所示：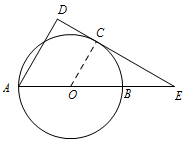
由切割线定理可得 $EC^2=EB\cdot EA$，即 $\left(2\sqrt 3\right)^2=EB\cdot \left(EB+4\right)$，解得 $EB=2$，所以 $O$ 是 $EA$ 靠近 $A$ 的三等分点．因为 $\angle OCE=\angle ADE=90^\circ $，所以 $OC\parallel AD$，所以 $\dfrac{OC}{AD}=\dfrac{EO}{AE}=\dfrac{2}{3}$，又 $OC=\dfrac{1}{2}AB=2$，$AE=6$，解得 $AD=3$．
由切割线定理可得 $EC^2=EB\cdot EA$，即 $\left(2\sqrt 3\right)^2=EB\cdot \left(EB+4\right)$，解得 $EB=2$，所以 $O$ 是 $EA$ 靠近 $A$ 的三等分点．因为 $\angle OCE=\angle ADE=90^\circ $，所以 $OC\parallel AD$，所以 $\dfrac{OC}{AD}=\dfrac{EO}{AE}=\dfrac{2}{3}$，又 $OC=\dfrac{1}{2}AB=2$，$AE=6$，解得 $AD=3$．
题目
答案
解析
备注
