已知 $\overrightarrow{e_1}$，$\overrightarrow{e_2}$ 是平面单位向量，且 $\overrightarrow{e_1}\cdot \overrightarrow{e_2}=\dfrac 12$．若平面向量 $\overrightarrow{b}$ 满足 $\overrightarrow{b}\cdot\overrightarrow{e_1} =\overrightarrow{b}\cdot\overrightarrow{e_2} =1$，则 ${\left|{\overrightarrow{b}}\right|}=$ ．
【难度】
【出处】
2015年高考浙江卷（文）
【标注】
【答案】
$\dfrac{2\sqrt 3}3$
【解析】
本题一定要注意向量数量积的投影的含义，再结合几何意义来解决．由 $ \overrightarrow {e_1}\cdot \overrightarrow {e_2}=\dfrac 12$ 和 $\overrightarrow{e_1}$，$\overrightarrow{e_2}$ 是平面单位向量可知，$\overrightarrow{e_1}$ 和 $\overrightarrow{e_2}$ 的夹角为 $60^\circ$．
又\[\overrightarrow{b}\cdot\overrightarrow{e_1} =1,\]所以 $\overrightarrow{b}$ 在 $\overrightarrow{e_1}$ 方向上的投影为 $1$，同理 $\overrightarrow{b}$ 在 $\overrightarrow{e_2}$ 方向上的投影也为 $1$．
于是可得，$\overrightarrow{b}$，$\overrightarrow{e_1}$，$\overrightarrow{e_2}$ 的位置关系如图所示．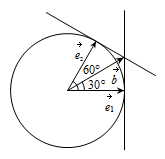
于是可得 ${\left|{\overrightarrow{b}}\right|}=\dfrac{2\sqrt 3}3$．
又\[\overrightarrow{b}\cdot\overrightarrow{e_1} =1,\]所以 $\overrightarrow{b}$ 在 $\overrightarrow{e_1}$ 方向上的投影为 $1$，同理 $\overrightarrow{b}$ 在 $\overrightarrow{e_2}$ 方向上的投影也为 $1$．
于是可得，$\overrightarrow{b}$，$\overrightarrow{e_1}$，$\overrightarrow{e_2}$ 的位置关系如图所示．
于是可得 ${\left|{\overrightarrow{b}}\right|}=\dfrac{2\sqrt 3}3$．
题目
答案
解析
备注
