椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\left(a>b>0\right)$ 的右焦点 $F\left(c,0\right)$ 关于直线 $y=\dfrac bcx$ 的对称点 $Q$ 在椭圆上,则椭圆的离心率是 .
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{\sqrt 2}2$
【解析】
本题要充分利用对称的条件,把 $QF$ 和 $QF_1$ 求出来,再结合椭圆的定义即可得到关于 $a$、$b$、$c$ 的方程,从而求得离心率.设椭圆左焦点为 $ F_1 $,连接 $ QF $ 交直线 $y=\dfrac bcx$ 于点 $ M $,连接 $ QF_1 $.因为 $ M $,$O $ 分别为 $QF $,$ F_1F $ 中点,所以\[ \dfrac {OM}{F_1Q}=\dfrac {MF}{FQ}=\dfrac {1}{2} .\]在 $ {\mathrm{Rt}}\triangle OMF $ 中,\[\tan \angle {MOF}=\dfrac {MF}{OM}=\dfrac {b}{c} ,且 OF=c , \]解得 $ OM=\dfrac {c^2}{a}$,$MF=\dfrac {bc}{a} $.因为 $Q $ 点在椭圆上,所以根据椭圆定义知\[ QF+QF_1=\dfrac {2bc }{a}+\dfrac {2c^2}{a}=2a, \]整理得 $ b=c$,所以 $ a=\sqrt 2c $,故椭圆的离心率是 $ e=\dfrac {c}{a}=\dfrac {\sqrt 2}{2} $.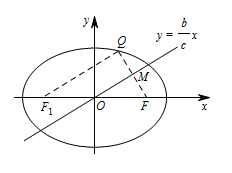

题目
答案
解析
备注