若实数 $x$,$y$ 满足 $x^2+y^2\leqslant 1$,则 ${\left|{2x+y-2}\right|}+{\left|{6-x-3y}\right|}$ 的最小值是 .
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
本题的重点在于去绝对值,不确定符号的要分类讨论,数形结合来解更容易,然后利用线性规划的内容来解决.在 $x^2+y^2\leqslant 1$时,$6-x-3y>0$,所以\[f\left(x,y\right)=\begin{cases}x-2y+4,\quad\quad y\geqslant -2x+2,\\ -3x-4y+8,\quad y<-2x+2.\end{cases}\]直线 $ y= -2x+2 $ 与圆 $ x^2+y^2=1 $ 相交于 $A $、$B $ 两点,如图所示,易得 $ A\left(1,0\right) $,$B\left(\dfrac 35,\dfrac 45\right) $.
设目标函数 $z_1=x-2y+4 $,$z_2=-3x-4y+8 $,它们所对的可行域分别为劣弧 $ {AB} $ 所对弓形和优弧 $ {BCA} $ 所对弓形,可知二者均在点 $B $ 处取得最小值 $ 3 $.所以 ${\left|{2x+y-2}\right|}+{\left|{6-x-3y}\right|}$ 的最小值是 $ 3 $.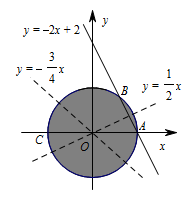
设目标函数 $z_1=x-2y+4 $,$z_2=-3x-4y+8 $,它们所对的可行域分别为劣弧 $ {AB} $ 所对弓形和优弧 $ {BCA} $ 所对弓形,可知二者均在点 $B $ 处取得最小值 $ 3 $.所以 ${\left|{2x+y-2}\right|}+{\left|{6-x-3y}\right|}$ 的最小值是 $ 3 $.

题目
答案
解析
备注