已知 $\overrightarrow{e_1}$，$\overrightarrow{e_2}$ 是空间单位向量，$\overrightarrow{e_1}\cdot \overrightarrow{e_2}=\dfrac 12$，若空间向量 $\overrightarrow{b}$ 满足 $\overrightarrow{b}\cdot\overrightarrow{e_1} =2$，$\overrightarrow{b}\cdot\overrightarrow{e_2} =\dfrac 52$，且对于任意 $x,y\in{\mathbb{R}}$，${\left|{\overrightarrow{b}-\left(x\overrightarrow{e_1}+y\overrightarrow{e_2}\right)}\right|}\geqslant {\left|{\overrightarrow b-\left(x_0\overrightarrow{e_1}+y_0\overrightarrow{e_2}\right)}\right|}=1$（$x_0,y_0\in{\mathbb{R}}$），则 $x_0=$ ，$y_0=$ ，${\left|{\overrightarrow{b}}\right|}=$ ．
【难度】
【出处】
无
【标注】
【答案】
$1$；$2$；$2\sqrt 2$
【解析】
本题的难点是抓住数量积的最小值，把空间向量问题转化为平面向量问题来处理．由题意得，$\langle \overrightarrow{e_1},\overrightarrow{e_2}\rangle=\dfrac{\mathrm \pi} {3}$．在向量 ${\overrightarrow e_1}$，$\overrightarrow e_2$ 所在的两条射线上分别取 $OM=2$，$ON=\dfrac 52$，分别过点 $M$、$N$ 作与射线 $OM$、$ON$ 垂直的平面，则向量 $\overrightarrow b$ 的终点 $Q$ 在这两个平面的交线上．记此交线与平面 $MON$ 的交点为 $P$．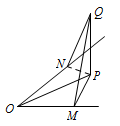
根据题意，向量 $x\overrightarrow e_1+y\overrightarrow e_2$ 的终点 $R$ 可以取遍整个平面 $MON$，此时\[|QR|=\left|\overrightarrow b-\left(x\overrightarrow e_1+y\overrightarrow e_2\right)\right|,\]其最小值为 $|QP|$，且 $|QP|=1$．
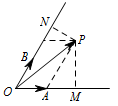此时分析平面 $MON$，可以得到 $\overrightarrow{OP}=\overrightarrow e_1+2\overrightarrow e_2$，于是 $x_0=1$，$y_0=2$．而\[\left|\overrightarrow b\right|^2=|OP|^2+|QP|^2=8,\]因此 $\left|\overrightarrow b\right|=2\sqrt 2$．
根据题意，向量 $x\overrightarrow e_1+y\overrightarrow e_2$ 的终点 $R$ 可以取遍整个平面 $MON$，此时\[|QR|=\left|\overrightarrow b-\left(x\overrightarrow e_1+y\overrightarrow e_2\right)\right|,\]其最小值为 $|QP|$，且 $|QP|=1$．此时分析平面 $MON$，可以得到 $\overrightarrow{OP}=\overrightarrow e_1+2\overrightarrow e_2$，于是 $x_0=1$，$y_0=2$．而\[\left|\overrightarrow b\right|^2=|OP|^2+|QP|^2=8,\]因此 $\left|\overrightarrow b\right|=2\sqrt 2$．
题目
答案
解析
备注
