如图，已知圆 $C$ 与 $x$ 轴相切于点 $T\left(1,0\right)$，与 $y$ 轴正半轴交于两点 $A$，$B$（$B$ 在 $A$ 的上方），且 ${\left|{AB}\right|}=2$．
$(1)$ 圆 $C$ 的标准方程为 ；
$(2)$ 圆 $C$ 在点 $B$ 处的切线在 $x$ 轴上的截距为 ．
$(1)$ 圆 $C$ 的标准方程为
$(2)$ 圆 $C$ 在点 $B$ 处的切线在 $x$ 轴上的截距为
【难度】
【出处】
2015年高考湖北卷（文）
【标注】
【答案】
$(1)$ $\left(x-1\right)^2+\left(y-\sqrt 2\right)^2=2$；$(2)$ $-\sqrt 2-1$
【解析】
本题考查直线与圆的位置关系，根据条件找出圆的圆心位置及半径大小，进而写出圆的方程．找 $AB$ 的中点 $D$，连接 $CD$，$CA$，$CB$，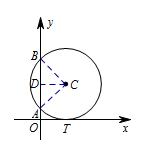
则 $AD=1$，又 $CD=OT=1$，所以圆的半径\[r=AC=\sqrt 2.\]又圆 $C$ 与 $x$ 轴相切于点 $T\left(1,0\right)$，所以圆心 $C$ 的横坐标与点 $T$ 的横坐标相同，纵坐标即半径 $r$，也即圆心坐标为 $\left(1,\sqrt 2\right)$，所以圆的方程为\[\left(x-1\right)^2+\left(y-\sqrt 2\right)^2=2.\]容易得出点 $B$ 的坐标 $\left(0,1+\sqrt 2\right)$，$CB$ 的斜率为 $k=-1$，所以圆 $C$ 在点 $B$ 处的切线的斜率为 $1$，切线方程为\[y-1-\sqrt 2=x,\]于是可得在 $x$ 轴上的截距为 $-\sqrt 2-1$．
则 $AD=1$，又 $CD=OT=1$，所以圆的半径\[r=AC=\sqrt 2.\]又圆 $C$ 与 $x$ 轴相切于点 $T\left(1,0\right)$，所以圆心 $C$ 的横坐标与点 $T$ 的横坐标相同，纵坐标即半径 $r$，也即圆心坐标为 $\left(1,\sqrt 2\right)$，所以圆的方程为\[\left(x-1\right)^2+\left(y-\sqrt 2\right)^2=2.\]容易得出点 $B$ 的坐标 $\left(0,1+\sqrt 2\right)$，$CB$ 的斜率为 $k=-1$，所以圆 $C$ 在点 $B$ 处的切线的斜率为 $1$，切线方程为\[y-1-\sqrt 2=x,\]于是可得在 $x$ 轴上的截距为 $-\sqrt 2-1$．
题目
答案
解析
备注
