如图，圆 $C$ 与 $x$ 轴相切于点 $T\left(1,0\right)$，与 $y$ 轴正半轴交于两点 $A$，$B$（$B$ 在 $A$ 的上方），且 ${\left|{AB}\right|}=2$．
（1）圆 $C$ 的标准方程为 ；
（2）过点 $A$ 任作一条直线与圆 $O:x^2+y^2=1$ 相交于 $M$，$N$ 两点，下列三个结论：
① $\dfrac{ \left|NA \right|}{ \left|NB \right|}=\dfrac{ \left|MA \right|}{ \left|MB \right|}$；② $\dfrac{ \left|NB \right|}{ \left|NA \right|}-\dfrac{ \left|MA \right|}{ \left|MB \right|}=2$；③ $\dfrac{ \left|NB \right|}{ \left|NA \right|}+\dfrac{ \left|MA \right|}{ \left|MB \right|}=2\sqrt 2$．
其中正确结论的序号是 ．（写出所有正确结论的序号）
（1）圆 $C$ 的标准方程为
（2）过点 $A$ 任作一条直线与圆 $O:x^2+y^2=1$ 相交于 $M$，$N$ 两点，下列三个结论：
① $\dfrac{ \left|NA \right|}{ \left|NB \right|}=\dfrac{ \left|MA \right|}{ \left|MB \right|}$；② $\dfrac{ \left|NB \right|}{ \left|NA \right|}-\dfrac{ \left|MA \right|}{ \left|MB \right|}=2$；③ $\dfrac{ \left|NB \right|}{ \left|NA \right|}+\dfrac{ \left|MA \right|}{ \left|MB \right|}=2\sqrt 2$．
其中正确结论的序号是
【难度】
【出处】
无
【标注】
【答案】
（1）$\left(x-1\right)^2+\left(y-\sqrt 2\right)^2=2$；（2）①②③
【解析】
本题利用参数方程来求解就可以避免大量的计算．（1）如图：设 $ AB $ 中点为 $D $，连接 $ CD $，$ CA $．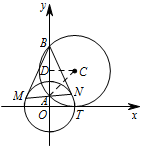
则 $ CD\perp AB$，且 $ |AD|=|CD|=1$，$\therefore r=|AC|=\sqrt 2 $．
$\because$ 圆 $C$ 与 $x$ 轴相切于点 $T\left(1,0\right)$，$\therefore$ $C\left(1,\sqrt 2\right) $，$\therefore$ 圆 $C $ 方程为 $\left(x-1\right)^2+\left(y-\sqrt 2\right)^2=2 $．
（2）由（1）可求得 $ A\left(0,\sqrt 2-1\right) $，$ B\left(0,\sqrt 2+1\right) $．
$\because M , N$ 两点在圆 $O:x^2+y^2=1$ 上，$\therefore$ 设 $ M\left(\cos \alpha,\sin \alpha\right) $，$ N\left(\cos \beta, \sin \beta\right) $．\[\begin{split}\therefore |NA|&\overset{\left[a\right]}=\sqrt{\cos ^2\beta+\left(\sin \beta-\sqrt 2+1\right)^2} \\&\overset{\left[b\right]}=\sqrt{2\left(\sqrt 2-1\right)\left(\sqrt 2-\sin \beta\right)},\\ |NB|&=\sqrt{\cos ^2\beta+\left(\sin \beta-\sqrt 2-1\right)^2}\\&=\sqrt{2\left(\sqrt 2+1\right)\left(\sqrt 2 -\sin \beta\right)} \end{split}\]（推导中用到：[a][b]）$\therefore \dfrac{ \left|NA \right|}{ \left|NB \right|}=\sqrt 2 -1 $．
同理可得 $ \dfrac{ \left|MA \right|}{ \left|MB \right|}=\sqrt 2-1 $．
故 ①②③ 均正确．
则 $ CD\perp AB$，且 $ |AD|=|CD|=1$，$\therefore r=|AC|=\sqrt 2 $．$\because$ 圆 $C$ 与 $x$ 轴相切于点 $T\left(1,0\right)$，$\therefore$ $C\left(1,\sqrt 2\right) $，$\therefore$ 圆 $C $ 方程为 $\left(x-1\right)^2+\left(y-\sqrt 2\right)^2=2 $．
（2）由（1）可求得 $ A\left(0,\sqrt 2-1\right) $，$ B\left(0,\sqrt 2+1\right) $．
$\because M , N$ 两点在圆 $O:x^2+y^2=1$ 上，$\therefore$ 设 $ M\left(\cos \alpha,\sin \alpha\right) $，$ N\left(\cos \beta, \sin \beta\right) $．\[\begin{split}\therefore |NA|&\overset{\left[a\right]}=\sqrt{\cos ^2\beta+\left(\sin \beta-\sqrt 2+1\right)^2} \\&\overset{\left[b\right]}=\sqrt{2\left(\sqrt 2-1\right)\left(\sqrt 2-\sin \beta\right)},\\ |NB|&=\sqrt{\cos ^2\beta+\left(\sin \beta-\sqrt 2-1\right)^2}\\&=\sqrt{2\left(\sqrt 2+1\right)\left(\sqrt 2 -\sin \beta\right)} \end{split}\]（推导中用到：[a][b]）$\therefore \dfrac{ \left|NA \right|}{ \left|NB \right|}=\sqrt 2 -1 $．
同理可得 $ \dfrac{ \left|MA \right|}{ \left|MB \right|}=\sqrt 2-1 $．
故 ①②③ 均正确．
题目
答案
解析
备注
