若直线 $3x-4y+5=0$ 与圆 $x^2+y^2=r^2\left(r>0\right)$ 相交于 $A$，$B$ 两点，且 $\angle AOB=120^\circ$（$O$ 为坐标原点），则 $r=$ ．
【难度】
【出处】
2015年高考湖南卷（文）
【标注】
【答案】
$2$
【解析】
与圆相关的弦满足，圆心与弦中点的连线垂直于弦，与之对应的直角三角形是解题的关键．由直线与圆相交，画出示意图如下，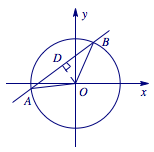
过点 $O$ 作 $OD\perp AB$ 于点 $D$，由点到直线距离公式，得\[|OD|=\dfrac{5}{\sqrt{3^2+4^2}}=1.\]由 $\angle AOB=120^\circ$，$OA=OB$，知 $\angle OPD=30^\circ$，则 $|OB|=2|OD|=2$，即 $r=2$．
过点 $O$ 作 $OD\perp AB$ 于点 $D$，由点到直线距离公式，得\[|OD|=\dfrac{5}{\sqrt{3^2+4^2}}=1.\]由 $\angle AOB=120^\circ$，$OA=OB$，知 $\angle OPD=30^\circ$，则 $|OB|=2|OD|=2$，即 $r=2$．
题目
答案
解析
备注
