若函数 $f\left(x\right)= \left|2^x-2 \right|-b$ 有两个零点，则实数 $b$ 的取值范围是 ．
【难度】
【出处】
2015年高考湖南卷（文）
【标注】
【答案】
$\left(0,2\right)$
【解析】
含参函数的零点问题可以通过参变分离，转化为两个函数的交点个数问题．“函数 $f\left(x\right)=|2^x-2|-b$ 有两个零点”等价于“函数 $y=|2^x-2|$ 与直线 $y=b$ 有两个交点”．
根据指数函数的图象和函数的图象变换，可画出 $y=|2^x-2|$ 与 $y=b$ 的图象如下图．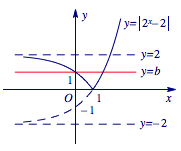
因此，当 $b\in\left(0,2\right)$ 时，函数 $y=|2^x-2|$ 与 $y=b$ 有两个交点，即函数 $f\left(x\right)$ 有两个零点．
根据指数函数的图象和函数的图象变换，可画出 $y=|2^x-2|$ 与 $y=b$ 的图象如下图．
因此，当 $b\in\left(0,2\right)$ 时，函数 $y=|2^x-2|$ 与 $y=b$ 有两个交点，即函数 $f\left(x\right)$ 有两个零点．
题目
答案
解析
备注
