已知 $\omega>0$，在函数 $y=2\sin {\omega x}$ 与 $y=2\cos {\omega x}$ 的图象的交点中，距离最短的两个交点的距离为 $2\sqrt 3$，则 $\omega=$ ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{\mathrm \pi} {2}$
【解析】
最短距离可能为图中的 $|AB|$ 或 $|AC|$，须分类考虑．注意到函数的周期性和对称性，只需要考虑两个函数在周期 $\left[0,\dfrac{2{\mathrm \pi} }{\omega}\right]$ 内的函数图象，如图．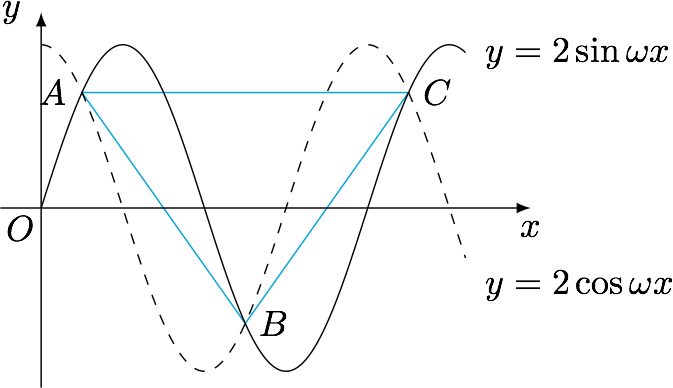
由于交点的横坐标即方程 $2\sin\omega x=2\cos\omega x$ 的解，可得 $\omega x=k{\mathrm \pi} +\dfrac{\mathrm \pi} 4$（$k\in{\mathbb Z}$），因此交点的纵坐标必然为 $\pm \sqrt 2$．如图，设相邻的三个交点为 $A\left(x_1,\sqrt 2\right)$，$B\left(x_2,-\sqrt 2\right)$，$C\left(x_3,\sqrt 2\right)$，则根据题意有（这是一个很容易被忽略的分类，很多地方给出的解答直接认为两个交点间的最短距离即为横坐标最接近的两个交点间的距离）\[\min\left\{|AB|,|AC|\right\}=2\sqrt 3,\]若 $|AB|=2\sqrt 3$，可得\[\left(\dfrac{\mathrm \pi} {\omega}\right)^2+\left(2\sqrt 2\right)^2=\left(2\sqrt 3\right)^2,\]解得 $\omega=\dfrac{\mathrm \pi} 2$，此时 $|AC|=\dfrac{2{\mathrm \pi} }{\omega}=4>2\sqrt 3$，符合题意．
若 $|AC|=2\sqrt 3$，可得 $\dfrac{2{\mathrm \pi} }{\omega}=2\sqrt 3$，此时\[|AB|=\sqrt{\left(\dfrac{\mathrm \pi} {\omega}\right)^2+\left(2\sqrt 2\right)^2}=\sqrt{11}<2\sqrt 3,\]不符合题意．因此 $\omega$ 的值为 $\dfrac{\mathrm \pi} {2}$．
由于交点的横坐标即方程 $2\sin\omega x=2\cos\omega x$ 的解，可得 $\omega x=k{\mathrm \pi} +\dfrac{\mathrm \pi} 4$（$k\in{\mathbb Z}$），因此交点的纵坐标必然为 $\pm \sqrt 2$．如图，设相邻的三个交点为 $A\left(x_1,\sqrt 2\right)$，$B\left(x_2,-\sqrt 2\right)$，$C\left(x_3,\sqrt 2\right)$，则根据题意有（这是一个很容易被忽略的分类，很多地方给出的解答直接认为两个交点间的最短距离即为横坐标最接近的两个交点间的距离）\[\min\left\{|AB|,|AC|\right\}=2\sqrt 3,\]若 $|AB|=2\sqrt 3$，可得\[\left(\dfrac{\mathrm \pi} {\omega}\right)^2+\left(2\sqrt 2\right)^2=\left(2\sqrt 3\right)^2,\]解得 $\omega=\dfrac{\mathrm \pi} 2$，此时 $|AC|=\dfrac{2{\mathrm \pi} }{\omega}=4>2\sqrt 3$，符合题意．若 $|AC|=2\sqrt 3$，可得 $\dfrac{2{\mathrm \pi} }{\omega}=2\sqrt 3$，此时\[|AB|=\sqrt{\left(\dfrac{\mathrm \pi} {\omega}\right)^2+\left(2\sqrt 2\right)^2}=\sqrt{11}<2\sqrt 3,\]不符合题意．因此 $\omega$ 的值为 $\dfrac{\mathrm \pi} {2}$．
题目
答案
解析
备注
