如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为 .

【难度】
【出处】
无
【标注】
【答案】
$1.2$
【解析】
建立坐标系求出抛物线方程,然后利用定积分求现在的截面面积.提示:建立如图所示的直角坐标系,易得抛物线为 $ y=\dfrac {2}{25}x^2-2 $.因为原始的最大流量与当前最大流量的比值为相应截面面积的比值,又四边形 $ ABCD $ 的面积为 $ 16 $ $ \mathrm m^2 $,四边形 $ ABCD $ 中除去阴影部分的面积为 $ \int_{-5}^5 \left(2-\dfrac {2}{25}x^2\right)\mathrm dx=\dfrac {40}{3} $ $ \mathrm m^2 $,所以所求比值为 $ 1.2$.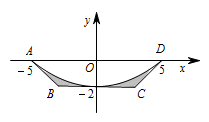

题目
答案
解析
备注