过点 $P\left(1,\sqrt 3\right)$ 作圆 $x^2+y^2=1$ 的两条切线,切点分别为 $A$,$B$,则 $\overrightarrow {PA}\cdot \overrightarrow {PB}=$ .
【难度】
【出处】
2015年高考山东卷(文)
【标注】
【答案】
$\dfrac 32$
【解析】
分析题中条件,由直线与圆的位置关系,可计算 $\overrightarrow{PA}$ 模长及两切线的夹角,问题即可解决.此题是圆的切线的相关问题与有向线段形式的数量积问题的综合.圆 $x^2+y^2=1$ 的圆心坐标为 $\left(0,0\right)$,半径为 $1$,所以由两点间距离公式得 $\left|OP\right|=2$.所以圆的切线长$\left|\overrightarrow {PA}\right|=\left|\overrightarrow {PB}\right|=\sqrt{|OP|^2-|OA|^2}=\sqrt 3$,$\angle APB=60^\circ$.故 $\overrightarrow{PA}\cdot\overrightarrow {PB}=\left|\overrightarrow{PA}\right|\cdot\left|\overrightarrow{PB}\right|\cdot \cos\angle APB=\dfrac{3}{2}$.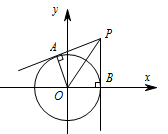

题目
答案
解析
备注