正三棱锥 $ABC-A_1B_1C_1$ 中，$AB=AA_1=1$，点 $P$ 满足 $\overrightarrow{BP}=\lambda\overrightarrow{BC}+\mu\overrightarrow{BB_1}$，其中 $\lambda\in[0,1]$，$\mu\in[0,1]$，则 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
BD
【解析】
\begin{center} \end{center}选项 $A$，$\overrightarrow{BP}=\overrightarrow{BC}+\mu\overrightarrow{BB_1} \Rightarrow \overrightarrow{CP}=\mu\overrightarrow{BB_1}$，故点 $P$ 在 $CC_1$ 上．将平面 $B_1BCC_1$ 与平面 $AA_1C_1C$ 沿着 $CC_1$ 展开，发现 $B_1P+PA$ 在变，周长 $=B_1P+PA+AB_1$ 不为定值．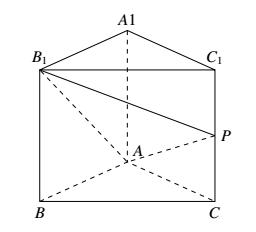
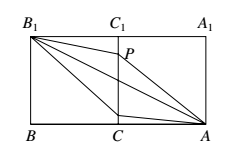\begin{center} \end{center}选项 $B$，$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\overrightarrow{BB_1} \Rightarrow \overrightarrow{B_1P}=\lambda\overrightarrow{BC}$，故点 $P$ 在 $B_1C_1$ 上，点 $P$ 所在的直线 $B_1C_1 \varparallel BC$，且 $B_1C_1 \notin $ 平面 $A_1BC$，所以 $B_1C_1 \varparallel \text{平面}A_1BC$，故 $P$ 到平面 $A_1BC$ 的距离为定值，而底面积 $A_1BC$ 为定值，故 $V_{P-A_1BC}$ 为定值．
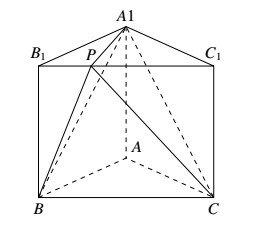选项 $C$，$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_1}$，如图所示，建立空间直角坐标系．设 $P(x_0,y_0,z_0)$，$B(\frac{1}{2},0,0)$，$C(0,\frac{\sqrt{3}}{2},0)$，$B_1(\frac{1}{2},0,1)$，$A_1(-\frac{1}{2},0,1)$ $\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_1}=(-\frac{1}{4},\frac{\sqrt{3}}{4},\mu)$，\qquad $\overrightarrow{BP}=(x_0-\frac{1}{2},y_0,z_0))$ 所以 $\left\{\begin{array}{l}x_0={\textstyle\frac14}\\y_0={\textstyle\frac{\sqrt3}4}\\z_0={\textstyle\mu}\end{array}\right.$ \qquad 所以，$P(\frac{1}{4},\frac{\sqrt{3}}{4},\mu-1)$ $\overrightarrow{A_1P}=(\frac{1}{4},\frac{\sqrt{3}}{4},\mu-1)$ \qquad 而 $\overrightarrow{A_1P}\cdot\overrightarrow{BP}=\frac{3}{16}+\frac{3}{16}+\mu^2-\mu=0$ \qquad 所以 $\mu=0,\text{或}1$．\begin{center} \end{center}
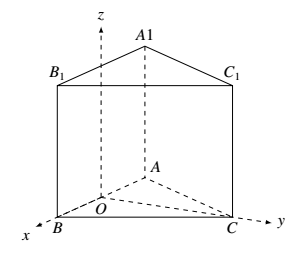选项 $D$，$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\frac{1}{2}\overrightarrow{BB_1}$，取 $BB_1$ 中点为 $K$，$\frac{1}{2}\overrightarrow{BB_1}=\overrightarrow{BK}$，$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\overrightarrow{BK}$，\qquad 所以 $\overrightarrow{KP}=\lambda\overrightarrow{BC}$．所以，$KP \varparallel BC$，取 $CC_1$ 中点 $L$，所以 $P\in KL$．$B(-\frac{1}{2},0,0)$，$B_1(-\frac{1}{2},0,1)$，$A(0,\frac{\sqrt{3}}{2},0)$，$A_1(0,\frac{\sqrt{3}}{2},1)$，$P(\lambda-\frac{1}{2},0,\frac{1}{2})$，$\overrightarrow{A_1B}=(-\frac{1}{2},-\frac{\sqrt{3}}{2},-1)$，$\overrightarrow{AB_1}=(-\frac{1}{2},\frac{\sqrt{3}}{2},1)$，$\overrightarrow{AP}=(\lambda-\frac{1}{2},-\frac{\sqrt{3}}{2},\frac{1}{2})$ \qquad $\left\{\begin{array}{l}\overrightarrow{A_1B\cdot}\overrightarrow{AB_1}=0\\\overrightarrow{A_1B_1\cdot}\overrightarrow{AP}=0\end{array}\right.$ \qquad 所以，$\frac{1}{2}-\frac{\lambda}{2}=0$，\qquad 所以 $\lambda=1$．故仅有一个点满足．选 $BD$．\begin{center} \end{center}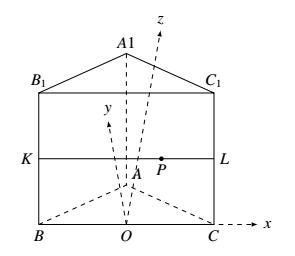
\begin{center} \end{center}选项 $B$，$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\overrightarrow{BB_1} \Rightarrow \overrightarrow{B_1P}=\lambda\overrightarrow{BC}$，故点 $P$ 在 $B_1C_1$ 上，点 $P$ 所在的直线 $B_1C_1 \varparallel BC$，且 $B_1C_1 \notin $ 平面 $A_1BC$，所以 $B_1C_1 \varparallel \text{平面}A_1BC$，故 $P$ 到平面 $A_1BC$ 的距离为定值，而底面积 $A_1BC$ 为定值，故 $V_{P-A_1BC}$ 为定值．选项 $C$，$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_1}$，如图所示，建立空间直角坐标系．设 $P(x_0,y_0,z_0)$，$B(\frac{1}{2},0,0)$，$C(0,\frac{\sqrt{3}}{2},0)$，$B_1(\frac{1}{2},0,1)$，$A_1(-\frac{1}{2},0,1)$ $\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_1}=(-\frac{1}{4},\frac{\sqrt{3}}{4},\mu)$，\qquad $\overrightarrow{BP}=(x_0-\frac{1}{2},y_0,z_0))$ 所以 $\left\{\begin{array}{l}x_0={\textstyle\frac14}\\y_0={\textstyle\frac{\sqrt3}4}\\z_0={\textstyle\mu}\end{array}\right.$ \qquad 所以，$P(\frac{1}{4},\frac{\sqrt{3}}{4},\mu-1)$ $\overrightarrow{A_1P}=(\frac{1}{4},\frac{\sqrt{3}}{4},\mu-1)$ \qquad 而 $\overrightarrow{A_1P}\cdot\overrightarrow{BP}=\frac{3}{16}+\frac{3}{16}+\mu^2-\mu=0$ \qquad 所以 $\mu=0,\text{或}1$．\begin{center} \end{center}选项 $D$，$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\frac{1}{2}\overrightarrow{BB_1}$，取 $BB_1$ 中点为 $K$，$\frac{1}{2}\overrightarrow{BB_1}=\overrightarrow{BK}$，$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\overrightarrow{BK}$，\qquad 所以 $\overrightarrow{KP}=\lambda\overrightarrow{BC}$．所以，$KP \varparallel BC$，取 $CC_1$ 中点 $L$，所以 $P\in KL$．$B(-\frac{1}{2},0,0)$，$B_1(-\frac{1}{2},0,1)$，$A(0,\frac{\sqrt{3}}{2},0)$，$A_1(0,\frac{\sqrt{3}}{2},1)$，$P(\lambda-\frac{1}{2},0,\frac{1}{2})$，$\overrightarrow{A_1B}=(-\frac{1}{2},-\frac{\sqrt{3}}{2},-1)$，$\overrightarrow{AB_1}=(-\frac{1}{2},\frac{\sqrt{3}}{2},1)$，$\overrightarrow{AP}=(\lambda-\frac{1}{2},-\frac{\sqrt{3}}{2},\frac{1}{2})$ \qquad $\left\{\begin{array}{l}\overrightarrow{A_1B\cdot}\overrightarrow{AB_1}=0\\\overrightarrow{A_1B_1\cdot}\overrightarrow{AP}=0\end{array}\right.$ \qquad 所以，$\frac{1}{2}-\frac{\lambda}{2}=0$，\qquad 所以 $\lambda=1$．故仅有一个点满足．选 $BD$．\begin{center} \end{center}
题目
答案
解析
备注
