由过右焦点的直线与渐近线平行，可得到此直线的方程，又点 $P$ 横坐标为 $2a$，且点 $P$ 既在双曲线上，又在直线上，即可得到 $a$，$b$，$c$ 的一个等式，又 $c^2=a^2+b^2$，有这两个等式，即可计算出离心率 $e$，问题得以解决．此题属于双曲线中确定离心率的问题．过右焦点且与渐近线平行的直线 $l$ 的斜率为 $\pm\dfrac ba$，则 $l$ 的方程为 $y=\pm\dfrac ba\left(x-c\right)$．点 $P$ 在曲线 $C$ 上，故将 $P$ 点横坐标代入双曲线方程中，解得 $P\left(2a,\pm \sqrt 3b\right)$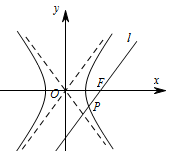，当 $l$ 斜率为正时，由图可知，$P$ 点的纵坐标为负，将 $P\left(2a,-\sqrt 3b\right)$ 代入直线 $l$ 的方程可得 $\dfrac{b} {a}\left(2a-c\right)=-\sqrt 3b$，解得离心率为 $e=\dfrac ca=2+\sqrt 3$．当 $l$ 斜率为负时，同理可解得离心率$e=\dfrac ca=2+\sqrt 3$．