一个六棱锥的体积为 $2\sqrt 3 $，其底面是边长为 $ 2 $ 的正六边形，侧棱长都相等，则该六棱锥的侧面积为 ．
【难度】
【出处】
2014年高考山东卷（文）
【标注】
【答案】
$12$
【解析】
考查空间正六棱锥的结构特征．正六棱锥的侧面是六个全等的等腰三角形，正六棱锥的顶点的射影是在底面的中心上，可构造直角三角形，计算出侧高，从而得到侧面积．由题意可知，题中六棱锥为正六棱锥，如图所示．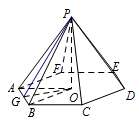
设正六棱锥 $P-ABCDEF$ 的高为 $h$，则其体积$V=\dfrac{1}{3}\cdot S_{底面积}\cdot h=\dfrac{1}{3}\cdot \dfrac{\sqrt 3}{4}\times 4\times 6\times h=2\sqrt 3$，解得 $h=1$．正六棱锥的斜高为 $h'=\sqrt{h^2+\left(\sqrt 3\right)^2}=2$．所以该棱锥的侧面积为 $S_{侧面积}=6\cdot \dfrac{1}{2}\cdot 2\cdot 2=12$．
设正六棱锥 $P-ABCDEF$ 的高为 $h$，则其体积$V=\dfrac{1}{3}\cdot S_{底面积}\cdot h=\dfrac{1}{3}\cdot \dfrac{\sqrt 3}{4}\times 4\times 6\times h=2\sqrt 3$，解得 $h=1$．正六棱锥的斜高为 $h'=\sqrt{h^2+\left(\sqrt 3\right)^2}=2$．所以该棱锥的侧面积为 $S_{侧面积}=6\cdot \dfrac{1}{2}\cdot 2\cdot 2=12$．
题目
答案
解析
备注
