圆心在直线 $x - 2y = 0$ 上的圆 $C$ 与 $y$ 轴的正半轴相切,圆 $C$ 截 $x$ 轴所得弦的长为 $2\sqrt 3 $,则圆 $C$ 的标准方程为 .
【难度】
【出处】
2014年高考山东卷(文)
【标注】
【答案】
${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 4$
【解析】
本题考查了直线与圆的位置关系,由直线与圆相切和直线与圆相交分别得到圆心坐标和半径,进而得到圆的标准方程.设圆 $C$ 的圆心坐标为 $\left(x_0,\dfrac{1}{2}x_0\right)$,因为圆 $C$ 与 $y$ 轴正半轴相切,所以 $x_0=r$,设圆 $C$ 与 $x$ 轴相交于 $A$,$B$ 两点,$D$ 为 $AB$ 的中点,所以 $r^2=CD^2+DB^2$,其中,$CD=\dfrac{r}{2}$,$DB=\sqrt 3$,于是,解得 $r=2$,因此,圆心坐标为 $\left(2,1\right)$.所以圆 $C$ 的标准方程$\left(x-2\right)^2+\left(y-1\right)^2=4$.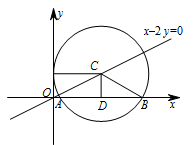
题目
答案
解析
备注