已知函数 $y = f\left(x\right)\left(x \in {\mathbb{R}}\right)$.对函数 $y = g\left(x\right)\left(x \in I\right)$,定义 $g\left(x\right)$ 关于 $f\left(x\right)$ 的"对称函数"为函数 $y = h\left(x\right)\left(x \in I\right)$,$y = h\left(x\right)$ 满足:对任意 $x \in I$,两个点 $\left(x,h\left(x\right)\right) $,$\left(x,g\left(x\right)\right)$ 关于点 $\left(x,f\left(x\right)\right)$ 对称.若 $h\left(x\right)$ 是 $g\left(x\right) = \sqrt {4 - {x^2}} $ 关于 $f\left(x\right) = 3x + b$ 的"对称函数",且 $h\left(x\right) > g\left(x\right)$ 恒成立,则实数 $b$ 的取值范围是 .
【难度】
【出处】
无
【标注】
【答案】
$\left(2 \sqrt {10} ,+\infty\right)$
【解析】
本题是一个创新小题,其突破点是“$h\left(x\right) > g\left(x\right)$ 恒成立”.$h(x)$ 是 $g(x)$ 关于直线 $f(x)$ 的对称函数,要求 $h(x)$ 恒大于 $g(x)$,故 $h(x)$ 横在 $g(x)$ 的上方,这就意味着,直线与 $g(x)$ 没有公共点且在 $g(x)$ 的图象上方,否则结合图象可推出不等式不恒成立.由题意,得 $\dfrac{{h\left( x \right) + \sqrt {4 - {x^2}} }}{2} = 3x + b$,则 $h\left( x \right) = 6x + 2b - \sqrt {4 - {x^2}} $.根据题意,得 $6x + 2b - \sqrt {4 - {x^2}} > \sqrt {4 - {x^2}} $,即 $3x + b > \sqrt {4 - {x^2}} $ 恒成立.在同一坐标系内,画出直线 $ y=3x+b$ 和半圆 $y = \sqrt {4 - {x^2}} $,如图所示,可得 $\dfrac{b}{{\sqrt {10} }} > 2$,即 $b > 2\sqrt {10} $.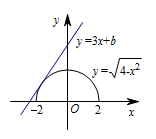
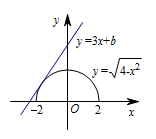
题目
答案
解析
备注