魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图,点 $E,H,G$ 在水平线 $AC$ 上,$DE$ 和 $FG$ 是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,$EG$ 称为“表距”,$GC$ 和 $EH$ 都称为“表目距”,$GC$ 与 $EH$ 的差称为“表目距的差”.则海岛的高 $AB=$ \((\qquad)\) .

【难度】
【出处】
无
【标注】
【答案】
A
【解析】
连接 $DF$ 交 $AB$ 于 $M$,则 $AB=AM+BM$.
记 $\angle BDM=\alpha, \angle BFM=\beta$,则 $\frac{MB}{\tan\beta}-\frac{MB}{\tan\alpha}=MF-MD=DF$.而 $\tan \beta=\frac{FG}{GC}, \tan\alpha=\frac{ED}{EH}$.所以$$\frac{MB}{\tan\beta}-\frac{MB}{\tan\alpha}=MB(\frac{1}{\tan\alpha}-\frac{1}{\tan\alpha})=MB\cdot (\frac{GC}{FG}-\frac{EH}{ED})=MB\cdot\frac{GC-EH}{ED}.$$故 $MB=\frac{ED\cdot DF}{GC-EH}=\frac{\text{表高}\times\text{表距}}{\text{表目距的差}}$,所以高 $AB=\frac{\text{表高}\times\text{表距}}{\text{表目距的差}}+\text{表高}$.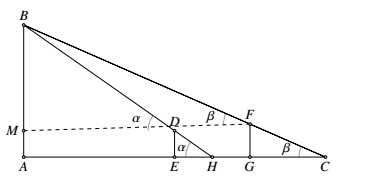
记 $\angle BDM=\alpha, \angle BFM=\beta$,则 $\frac{MB}{\tan\beta}-\frac{MB}{\tan\alpha}=MF-MD=DF$.而 $\tan \beta=\frac{FG}{GC}, \tan\alpha=\frac{ED}{EH}$.所以$$\frac{MB}{\tan\beta}-\frac{MB}{\tan\alpha}=MB(\frac{1}{\tan\alpha}-\frac{1}{\tan\alpha})=MB\cdot (\frac{GC}{FG}-\frac{EH}{ED})=MB\cdot\frac{GC-EH}{ED}.$$故 $MB=\frac{ED\cdot DF}{GC-EH}=\frac{\text{表高}\times\text{表距}}{\text{表目距的差}}$,所以高 $AB=\frac{\text{表高}\times\text{表距}}{\text{表目距的差}}+\text{表高}$.

题目
答案
解析
备注